Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas adicionais - Ex. 96
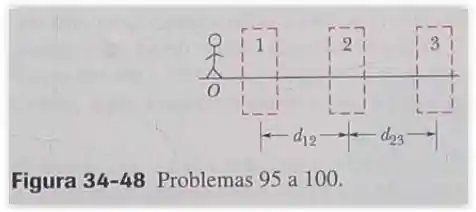
Sistema de três lentes. Na Fig. 34-48, o boneco (o objeto) está sobre o eixo central comum de três lentes delgadas simétricas, que estão montadas nas regiões limitadas por linhas tracejadas. A lente 1 está montada na região mais próxima de , a uma distância do boneco. A lente 2 está montada na região do meio, a uma distância da lente 1. A lente 3 está montada na região mais afastada de , a uma distânci da lente 2. Cada problema da Tabela 34-10 se refere uma combinação diferente de lentes e a valores diferentes das distâncias que são dadas em centímetros. O tipo de lente é indicado como no caso de uma lente convergente e como no caso de uma lente divergente; o número que se segue a ou é a distância entre a lente e um dos pontos focais (o sinal da distância focal não está indicado).
Determine
- A distância entre o objeto e imagem produzida pela lente 3 (a imagem final produzida pelo sistema)
- A ampliação lateral total do sistema, incluindo o sinal.
- Determine também se a imagem final é real (R) ou virtual (V)
- Se é invertida (I) ou não invertida (NI)
- Se está do mesmo lado da lente que o objeto (M) ou está do lado oposto (O).
Passo 1
Na Tabela 34-10 vamos tirar algumas informações necessárias para resolver nosso problema.
; ; ;;;
Como estamos lidando com lentes delgadas, podemos desconsiderar o raio de curvatura e aplicar a Eq. 34-9
Para o cálculo da ampliação lateral, podemos fazer uso da Eq. 34-7
Passo 2
- Das informações obtidas da tabela, podemos assumir que as distâncias focais são , e
- Conhecendo os valores de e , podemos determinar a ampliação lateral Total do nosso problema. Entretanto vamos recordar que a Ampliação Total é dada pelo produto das ampliações de cada lente Eq.34-11
- Considerando o sinal de , dizendo que a imagem final é dita Virtual, pois se forma do mesmo lado que nosso objeto. Devemos lembrar que lentes convergentes podem formar imagens reais ou virtuais, enquanto lentes divergentes só formam imagens virtuais.
- Quando uma imagem é formada do lado oposto à do objeto, ou seja, ela é real, temos que ela é dita invertida (I), caso contrário temos uma imagem que é dita Não Invertida (NI). Pois bem, vamos analisar passo a passo nossa imagem. Para a primeira lente é divergente, logo só forma imagem virtual, e por sua vez Não Invertida. A segunda lente é convergente e temos que sua imagem é formada em , logo a lente 2 inverte a imagem. Por fim temos a lente 3 onde a imagem é formada em cima do foco, assim dizemos que ela não chegou a ser invertida e consequentemente a imagem real se inverteu apenas uma vez, logo ela é dita invertida
- Vamos olhar apenas para a lente 3 e no sistema de coordenada dela, tome que indicando que a imagem se forma do mesmo lado que a lente e o objeto (M).
Aplicando a Eq. 34-9 para a primeira lente, temos
Tomando que para a lente 2 a nova distância é definida pela imagem formada, e definida como
E novamente aplicando Eq.34-9 temos
E por fim, novamente Eq.34-9
Passo 3
Passo 3
Passo 4
Passo 5
Resposta
- A imagem é virtual (V)
- A imagem é invertida (I)
- A imagem é formada do mesmo lado da lente (M)