Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.4 - Ex. 16
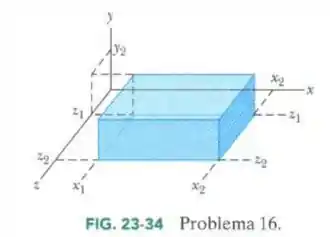
A superfície gaussiana em forma de paralelepípedo da Fig. 23-34 envolve uma carga de + 24,0ε0 C e está imersa em um campo elétrico dado por , com x e z em metros e b constante. A face inferior está no plano xz; a face superior está no plano horizontal que passa pelo ponto y2= 1,00 m. Qual é o valor de b para x1 = 1,00 m, x2 = 4,00 m, z1 = 1,00 m, z2 = 3,00 m?
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei ajudando você a resolver essa atividade.
Queremos aqui basicamente encontrar o valor de b para qual o valor do campo elétrico dado quando .
Para achar o valor de , podemos calcular o fluxo total do campo elétrico, através da superfície dada pela figura.
Temos a fórmula integral para o fluxo elétrico:
Para calcular essa integral vamos separar pelas faces do paralelepípedo.
Passo 2
Para as faces onde o fluxo é paralelo ao plano , ou seja, a face superior e a inferior, temos:
Lembrando que como é normal a superfície, e o produto de uma superfície que está no plano xy é na direção .
Agora para o plano xz:
Por fim, para o plano yz:
Passo 3
Finalmente!! Podemos utilizar a lei de Gauss para determinar o fluxo elétrico:
portanto: