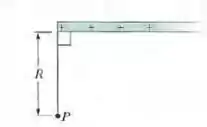
Na Fig. 22-52, uma barra não condutora "semi-infinita" (ou seja, infinita apenas em um sentido) possui uma densidade linear de cargas uniforme . Mostre que o campo elétrico no ponto faz um ângulo de com a barra e que o resultado não depende da distância . (Sugestão: calcule separadamente as componentes de na direç��o paralela à barra e na direção perpendicular à barra.)
Passo 1
Fala aí, galerinha! 😎

Nesse problema temos uma barra não condutora "semi-infinita" (ou seja, infinita apenas em um sentido) que possui uma densidade linear de cargas uniforme .
Nosso objetivo é mostrar que o campo elétrico no ponto faz um ângulo de com a barra e que o resultado não depende da distância
Tem ideia de como fazemos isso? 🤔
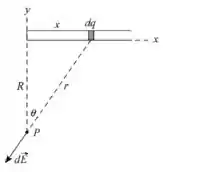
Vamos considerar um elemento bem pequeno da barra, chamaremos de e ele está a uma distância da extremidade esquerda da barra, como está na figura abaixo:
Veja só! 👀
Passo 2
Esse campo elétrico gerado por esse pedacinho infinitesimal de carga é dada por
E para encontrar o campo elétrico total, precisamos integrar todos os campos elétricos gerados por todos os pedacinhos de carga...
Mas não vamos conseguir integrar em função de , para tirar ele dali, faremos o seguinte...
Como a densidade de carga é linear, ou seja:
Onde é a carga total e o tamanho da barra.
Como temos que essa barra está uniformemente distribuída, podemos dizer que essa relação é válida para qualquer pedaço de carga por qualquer pedaço de comprimento, sendo assim, vamos pegar um pedaço infinitesimal de carga para podermos integrar.
Esse pedaço infinitesimal de comprimento está no eixo x e por isso pode ser dado como:
Substituindo, teremos:
Agora voltamos para a nossa expressão:
Só que temos um problema para integrar esse cara aqui. Esses vários vetores possuem direções diferentes, pois para cada pedacinho de carga, o vetor aponta numa direção diferente. Quando isso acontece, precisamos decompor o vetor, e então iremos calcular a soma das componentes horizontais e a das componentes verticais.
E assim, encontraremos o vetor campo elétrico.
Tranquilo até aqui? 😉
Passo 3
Lembre-se que o vetor campo elétrico se afasta da barra, pois ela tem carga positiva e, portanto, tem campo divergente (cargas positivas tem linhas de campo elétrico que saem da barra):
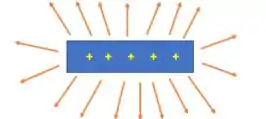
Agora, precisamos achar as componentes x e y do vetor campo elétrico. Para isso, basta a gente decompor nos eixos x e y. Vamos dar uma olhada na decomposição desse vetor?
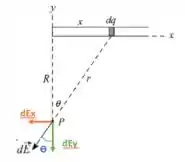
Podemos dizer que as componentes do vetor campo elétrico são:
E
Substituindo o valor que calculamos de :
Ai você me pergunta o motivo de estar negativo. Bem simples, percebe que nossa referência de eixo no desenho é positivo quando direcionado para cima e positivo quando direcionado para direita, como no nosso caso o vetor está direcionado para a esquerda, ele assume um valor negativo!
A outra componente do vetor campo elétrico é:
E também é negativa pelo mesmo motivo ;)
Passo 4
Para achar o campo elétrico da barra toda, e não de apenas um elemento dela, devemos integrar em toda a barra. Usaremos como a variável de integração, ok? Olhe para a figura do passo 1:
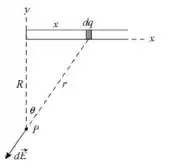
Vemos que
Logo:
e
Isto é:
Diferenciando essa última expressão, obtemos:
Como a barra é semi-infinita, os limites de integração são e , integrando:
Substituindo o valor que encontramos para :
Substituindo a expressão de :
Substituindo :
Dividindo por :
Arrumando essa fração:
Vamos dividir por :
Como :
Estamos quase lá! 😁
Passo 5
Vamos colocar tudo que não depende de para fora da integral:
Ufa, encontramos nossa componente em do vetor campo elétrico. Vamos agora para a componente em !
Mas não precisa fazer tudo de novo, é só se ligar!
Fazendo o mesmo para a componente teremos a mesma expressão, apenas trocando o por antes de integrar:
Logo
Vamos continuar! 😐
Passo 6
Olhe que, como :
Para qualquer valor de , o ângulo que o campo elétrico faz com a barra é de 45°, pois esse é o único ângulo que tem a propriedade de ter as componentes e iguais.
E aí! o que achou? Responde Aí! 😉
