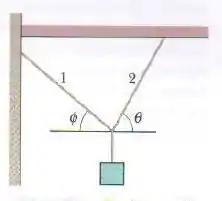
Na Figura um pacote de massa m está pendurado em uma corda que, por sua vez, está presa à parede através da corda 1 e ao teto através da corda 2 . A corda 1 faz um ângulo φ = 40 ° com a horizontal; a corda 2 faz um ângulo θ . (a) Para que valor de θ a tensão da corda 2 é mínima? (b) Qual é a tensão mínima da corda 2 , em múltiplos de m g ?

(a) θ = 55 ° (b) T 2 = 0,77m g

Enunciado

Vamos começar desenhando a situação:

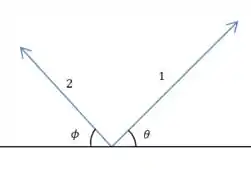
Vamos começar decompondo as componentes horizontais dos vetores, e usando a condição de equilíbrio:

E as componentes verticais, também pela condição de equilíbrio:

Com essas duas equações, chegamos ao seguinte sistema:

Como queremos saber qual valor de minimiza a tensão , vamos tentar isolar essa grandeza.

Começamos isolando na primeira equação:

E agora substituindo isso na segunda:

E assim fica:

Falta agora achar o valor de que minimiza essa função:

Plotando um gráfico dessa função:

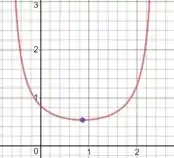
O ponto mínimo tem abcissa , que equivale a .

Por fim, para responder qual é a tensão mínima da corda, basta calcular quando .

E não precisamos saber a massa, já que o enunciado pede a resposta em unidades de .

Pronto!

(a)

(b)