Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.3 - Ex. 20

Um taco golpeia uma bola de golfe em uma pequena elevação acima do solo com uma velocidade de 12,0 m/s e um ângulo inicial de 51,0 ° acima da horizontal. A bola atinge o campo 2,08s após a tacada. Despreze a resistência do ar. a) Quais são os componentes da aceleração da bola durante o vôo? b) Quais são os componentes da velocidade da bola no início e no final de sua trajetória? c) Qual é a distância horizontal percorrida pela bola? d) Por que a expressão de R obtida no Exemplo 3.8 não pode ser usada para dar a resposta correta do item (c)? e) Qual era a altura da bola no momento em que ela saiu do taco? f) Faça diagramas x t ,   y t ,   v x t   e   v y t para o movimento.

Passo 1

Fala aí! tudo certinho?

Nesse problema temos uma bola de golfe que é golpeada a uma altura y 0 e adquire uma velocidade inicial de 12 m / s com um ângulo de 51 ° com a horizontal. A bola atinge o campo 2,08 s após ser golpeada.

A partir daí queremos saber quais são os componentes da aceleração da bola durante o vôo, as componentes da velocidade da bola no início e no final de sua trajetória, a distância horizontal percorrida pela bola, por que a expressão de R obtida no Exemplo 3.8 não pode ser usada para dar a resposta correta do item (c) e qual era a altura da bola no momento em que ela saiu do taco.

Bastante coisas, não é?

Veja só!

Passo 2

Nós vamos tomar como + y para cima

  1. Se a resistência do ar deve ser ignorada, os componentes da aceleração são 0 horizontalmente: a x = 0 ;

    2. E a y = - g = - 9,80   m / s 2 verticalmente para baixo.

    Bacana, não é?

    Passo 3

  2. A componente x da velocidade é constante em:

    3. v x = 12 m / s ⋅ cos ⁡ 51 ° = 7,55 m / s

    Na componente y , encontramos a velocidade inicial,

    v 0 y = 12 m / s ⋅ sen ⁡ 51 ° = 9,32 m / s

    no lançamento e:

    v y = v 0 y - g t  

    v y = 9,32   m / s - 9,8 m / s 2 ⋅ 2,08 s = - 11,06   m / s

    quando o taco bate.

    Tranquilo até aqui?

    Passo 4

  3. Para encontrarmos a distancia horizontal percorrida pela bola, temos que:

    4. ∆ x = v 0 x t = 7,55 m / s ⋅ 2,08 s  

    ∆ x = 15,7 m

    Show?

    Passo 5

  4. Pois as alturas inicial e final não são as mesmas.

    5. Concorda?

    Passo 5

  5. Com y = 0 e v 0 y = 9,32 m / s , partimos da equação:

    6. y = y 0 + v 0 y t - g t 2 2

    ⇒ y 0 = 1,81 m

    Estamos quase lá!

    Passo 6

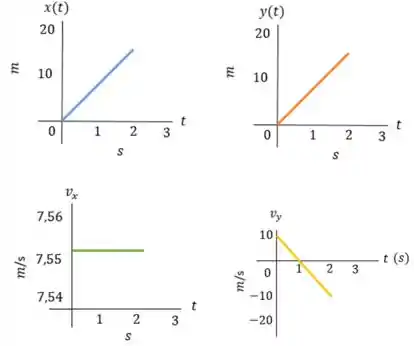
  6. Dessa forma, temos que os gráficos são:

E aí! entendeu tudo? Responde Aí!

Resposta

  1. a x = 0 e a y = - 9,80   m / s 2
  2. v x = c o n s t a n t e = 7,55 m / s ; v 0 y = 9,32 m / s e v y = - 11,06   m / s
  3. ∆ x = 15,7 m
  4. Pois as alturas inicial e final não são as mesmas.
  5. y 0 = 1,81 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um rifle que atira balas a 460   m / s é apontado para um alvo situado a 45,7   m de distância. Se o centro do alvo está na mesma altura do rifle, para que altura acima do alvo o cano do rifle deve se
Uma pedra é lançada por uma catapulta no instante t= 0 , com uma velocidade inicial de módulo 20,0m / s e ângulo 40,0 ° acima da horizontal. Quais são os módulos das componentes (a) horizontal e (b) v
Um garoto atira uma pedra com velocidade inicial de 15 m/s, a um ângulo de 60 ° com a horizontal.A) Qual é a altura máxima atingida pela pedra?B) Qual é o módulo da sua velocidade no ponto de altura m
Qual é o módulo da velocidade do projétil cujo movimento é visto na Figura 4.12 ao colidir contra o piso?
A Figura 4.12 mostra dados sobre um projétil que atinge um ponto em um plano elevado de uma altura H em relação ao ponto de lançamento. Quanto vale H?