Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 4.Exercícios e Problemas - Ex. 13

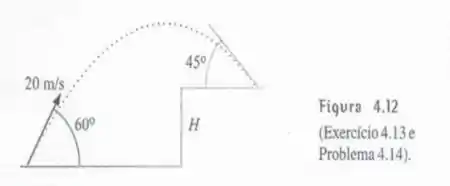
Qual é o módulo da velocidade do projétil cujo movimento é visto na Figura 4.12 ao colidir contra o piso?

Passo 1

Meus queridos...

Sabemos que:

v y 2 = v o y 2 - 2 g H

v y = v o ∙ s e n 60 ° 2 - 2 g H

Aplicando:

v y = 300 - 20 H

Sabemos que a equação do tempo de subida é dada por:

t s = v o ∙ s e n 45 ° g

t s = 2 2 ∙ 300 - 20 H 10 = 6 00 - 4 0 H 20

Vamos considerar a equação:

h = g t 2 2

h = g 2 600 - 40 H 20 2

Encontraremos que:

h = 15 - H 2

Passo 2

Conhecendo a equação:

h = v o y ∙ t - g t 2 2

h = v o ∙ s e n 60 ° ∙ 600 - 40 H 20 - 5 600 - 40 H 20 2

h = 20 ∙ 3 2 ∙ 4 h 20 - 5 ∙ 4 h 400

h = 12 h 2 - h 20

21 h 20 = 12 h 2

2,1 h 2 = 12 h

4,41 h 2 = 12 h

h = 2,72   m

Passo 3

Vamos pegar a nossa equação inicial:

v y = 300 - 20 H

Sabendo que:

300 - 20 H = 40 h

v y = 40 h

v y = 10,43   m / s

Sabemos que:

v y = v ∙ s e n ( 45 ° )

Então, aproximadamente:

v y = 14,1   m / s

Resposta

v y = 14,1   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um dublê dirige um carro a 20 m/s em direção à beira de um penhasco de 30 m de altura. A estrada que leva ao penhasco é inclinada para cima em um ângulo de 20°.a. A que distância da base do penhasco o
Um gato está caçando um camundongo. Este corre em linha reta com velocidade de 1,5 m/s. Se o gato salta do piso em um ângulo de 30° e com rapidez igual a 4,0 m/s, de que distância atrás do camundongo
Você se encontra a 6,0m da parede de uma casa e deseja arremessar uma bola para seu colega que está a 6,0m da parede oposta. Tanto o arremesso acima do solo quanto a interceptação da bola ocorrem 1,0m
Os cavaleiros do rei Artur disparam um canhão do topo da muralha de um castelo. A bala de canhão é disparada com 50 m/s em um ângulo de 30º. Outra bala de canhão, que foi acidentalmente deixada cair,
Os navios A e B deixam o porto simultaneamente. Nas próximas duas horas, o navio A navega a 20 mph para 30° a oeste do norte, enquanto o navio B navega para 20° a leste do norte a 25 mph.Qual é a dist