Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 53
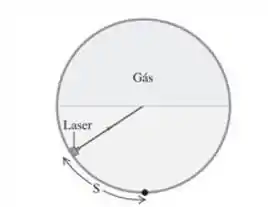
Um tanque cilíndrico horizontal com de diâmetro contém água até a metade. O espaço acima da água é preenchido com um gás pressurizado de indice de refração desconhecido. Um pequeno laser pode se mover ao longo do fundo curvo da água e lança um feixe de luz na direção do centro da superficie da água (Figura 33.51). Voce observa que, quando o laser se moveu uma distância ou mais (medida sobre a superficie curva) a partir do ponto mais baixo da água, nenhuma luz entra no gás. a) Qual é o indice de refração do gás? b) Quanto tempo leva para o feixe de luz se deslocar do laser até a borda do tanque quando: (i) ; (ii) ?
Passo 1
a)
se naquela posição o feixe de luz não passa para o gás ocorreu, portanto, a reflexão interna total. Aplicando a lei de snell:
O índice de refração do gás será dado por:
Eita...
Não sabemos quanto vale . Mas relaxa! Podemos descobrir!
O ângulo pode ser encontrado através do raio, , e de .
Show!
Então
É isso aí! Bora para a próxima!
Passo 2
b)
‘i) Na primeira situação, teremo um ângulo maior do que o ângulo crítico, já que . Dessa forma, o feixe não passará para o gás, e portanto ele irá percorrer todo o caminho na água. A distância percorrida será de até ele atingir a borda do cilindro.
A velocidade do feixe na água é;
Show! E o tempo de percurso pode ser encontrado a partir de;
Substituindo os valores, encontramos:
Tranquilo?
Passo 3
B)
ii)
Agora, o raio vai passar tanto pela água, como pelo gás. Ele vai percorrer um distância de na água e outra distância no gás. Vamos encontrar o tempo de cada etapa desse percurso e depois, vamos somar!
Etapa 1- na água:
Então, o tempo gasto na água é:
Etapa 2 – no gás:
Então, o tempo gasto nno gás é:
Show! Então o tempo total é;
Show!!
Resposta
a)
b)
i)
ii)