Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 56

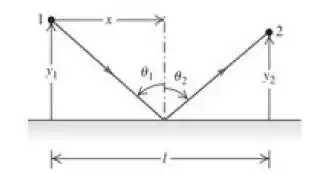
Um raio de luz deslocando-se com velocidade c parte do ponto 1 da Figura 33.54 é refletido no ponto 2. O raio atinge a superfície a uma distância horizontal x do ponto 1. a) Demonstre que o tempo t necessário para a luz se deslocar de 1 até 2 é dado por

t = y 1 2 + x 2 + y 2 2 + l - x 2 c

b) Faça a derivada de t em relação a x . Iguale a zero a derivada para mostrar que esse tempo atinge o valor mínimo quando θ 1 = θ 2 , que é a lei da reflexão e corresponde à trajetória real do raio. Trata-se do princípiclo tempo mínimo formulado por Fermat, segundo o qual, entre as trajetórias possíveis ligando dois pontos, aquela que realmente ocorre é a que gasta um tempo de percurso mínimo. (Contudo, existem alguns casos em que o tempo é máximo em vez de mínimo.)

Passo 1

a)

Aqui queremos saber o tempo de percurso que a luz demorou para fazer desde o ponto 1 até o ponto 2.

Sabemos que

v = Δ S Δ t

Então:

t = Δ S c

Só temos que decobrir o deslocamento. Para isso, vamos analisar os dois triângulos retângulos formados na figura.

Quando o raio está “descendo”, temos que o deslocamento pode ser encontrado pelo teorema de pitágoras:

d 1 = y 1 2 + x 2

E quando o raio está “subindo”:

d 2 = y 2 2 + l - x 2

Beleza! A distância total é d 1 + d 2

t = d 1 + d 2 c

t = y 1 2 + x 2 + y 2 2 + l - x 2 c

Show! Vamos para e letra b!

Passo 2

b)

Vamos derivar aquela equação em relação a x , e confirmar o príncipio de Fermat do tempo mínimo.

d t d x = 1 c 1 2 2 x y 1 2 + x 2 + 1 2 2 ( - 1 ) ( l - x ) y 2 2 + l - x 2    

Arrumando

d t d x = 1 c x y 1 2 + x 2 + ( - 1 ) ( l - x ) y 2 2 + l - x 2    

e igualando à zero, pois queremos verificar a situação de mínimo da função:

x y 1 2 + x 2 = ( l - x ) y 2 2 + l - x 2

Olhando para a figura percebemos que essa igualdade nada mais é do que:

sen ⁡ θ 1 = sen ⁡ θ 2

E isso acontece quando temos

θ 1 = θ 2

Maravilha!

Resposta

a) t = y 1 2 + x 2 + y 2 2 + l - x 2 c

b) demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ângulo de incidência θ a , na Figura 33.59 é escolhido de modo que o raio luminoso passe simetricamente através do prisma, cujo indice de refração é n e o ângulo do vértice é A. a) Mostre que o ângu
Uma lâmina de vidro de faces planas paralelas tem um índice de refração n e espessura h . Um raio de luz incide sobre ela com ângulo de incidência θ 1 ,. Mostre que o raio transmitido através da lâmin
Relacione δ no Probl. 6 com n e θ 1 , no caso geral (sem supor α e θ 1 pequenos), e mostre que δ é mínimo quando o ângulo de emergência θ 1 ' (fig. abaixo)é igual a θ 1 . Mostre que, quando isso acont
Considere um prisma de ângulo de abertura α e um raio incidente sobre uma face com ângulo de incidênciaθ 1 : seja n o índice de refração do prisma. Chama-se desvio δ o ângulo entre as direções do raio
Uma esfera transparente de índice de refração n , espelhada numa calota A B da sua superfície, com centro em C (fig.), é usada como retro-refletor: qualquer raio 1 paralelo ao eixo C D e paraxial (pró