Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.2 - Ex. 20a
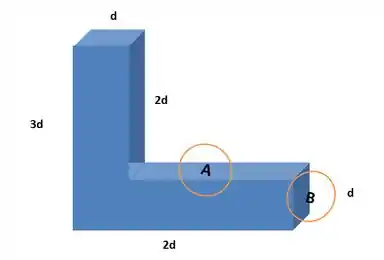
O tanque em forma de L mostrado na Figura está cheio d’água e é aberto na parte de cima. Se , qual é a força exercida pela água: (a) Na face e (b) Na face ?
Passo 1
Falaaa galerinha bonita, belezoca de motoca?
O enunciado nos deu que o tanque a seguir está cheio de água até a topo.
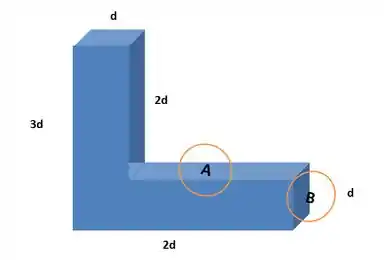
O tanque é aberto na parte de cima, e sendo , o enunciado quer que a gente encontre a força exercida pela agua sobre a face .
Então saca só, vamos primeiro precisar lembrar que a força hidrostática exercida por uma coluna de líquido de altura é dada por:
A gente somou a pressão atmosférica por que a caixa está aberta na parte de cima.
Lembrando que:
Passo 2
A força exercida pelo líquido sobre a superfície é dada por:
E como a pressão é dada de acordo com a altura :
Sendo assim, obtemos que a força será:
Como , obtemos que: