Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 9.Problemas - Ex. 2
Na teoria corpuscular da luz, no século 17, imaginava-se um feixe de luz como constituído de corpúsculos muito pequenos, movendo-se com velocidade muito elevada. A reflexão da luz num espelho seria produzida pela colisão dos corpúsculos luminosos com o mesmo, de forma análoga a uma colisão elástica com uma parede impenetrável. Ao atravessar a superfície de separação entre dois meios transparentes distintos (ar e água, por exemplo). um corpúsculo luminoso teria sua velocidade alterada pelo efeito de uma força impulsiva normal à superfície de separação, prosseguindo depois em seu movimento, livre da ação de forças. Sejam , e os ângulos de incidência, reflexão, e refração respectivamente. Mostre que este modelo explicaria as leis da reflexão e da refração: raios refletido e refratado no plano de incidência, com , , e calcule o índice de refração relativo do segundo meio em relação ao primeiro em função das velocidades dos corpúsculos nos meios 1 e 2. A velocidade dos corpúsculos seria maior no ar ou na água?
Passo 1
Vamos começar pela reflexão. Esse esquema aqui representa nossa situação
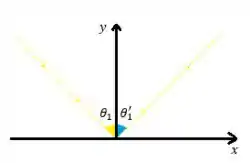
- O momento inicial dos corpúsculos era de
- O momento Final dos corpúsculos é de
(Nesse caso o coseno está na vertical e o seno na horizontal)
Pela conservação do momento
Como pela colisão ser elástica temos
Concluímos que
Passo 2
Já pela refração podemos visualizar assim
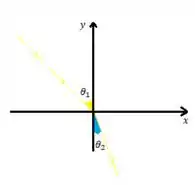
Sabemos que a partícula mudou seu momento devido a uma força na direção , mas na direção ele se conserva, então vamos analisar essa componente
Como o ângulo é maior então . Logo a velocidade seria maior na água.