Para explicar a resistência do ar (mais geralmente, de qualquer fluido) ao movimento de um corpo através dele, Newton propôs o seguinte modelo. O fluido é imaginado como sendo composto de um grande número (n por unidade de volume) de partículas em repouso, de massa m (muito pequena) cada uma. Quando o corpo, de massa M>>m, se desloca com velocidade v através do fluido, ele vai colidindo com as partículas e vai lhes transferindo momento dessa forma. A força F de resistência do fluido resultante é proporcional ao quadrado da velocidade. Calcule essa força se o corpo é uma placa de área A que se desloca perpendicularmente ao plano da placa, como função de A,v e da densidade nm do fluido.

Supondo ser uma colisão elástica e as partículas do fluído só ganham energia do tipo cinética e não térmica, podemos escrever a seguinte equação

Como as partículas do fluido estavam inicialmente em repouso então . Agora, a massa da placa é muito maior que a de uma pedacinho de massa do fluido, de massa . Ou seja,

Então fica assim

Como é o momento final da partícula do fluido e a velocidade da placa temos

Como o momento total tem que se conservar o momento transferido à placa é

Usando a segunda lei de Newton,

Vamos imaginar que esse pequeno elemento de massa empurrado seja uma fina camada de fluido em frente à placa, dessa forma aqui

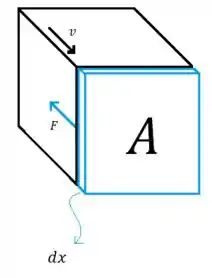
Na medida em que a placa se desloca com velocidade a fina massa é deslocada de , então podemos reescrever assim

Substituindo na fórmula temos