Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 7.Problemas - Ex. 3
Uma tira bimetálica, usada para controlar termostatos, é constituída de uma lâmina estreita de latão, de de espessura, presa lado a lado com uma lâmina de aço, de mesma espessura , por uma série de rebites. A , as duas lâminas têm o mesmo comprimento, igual a , e a tira está reta. A extremidade da tira é fixa; a outra extremidade pode mover-se, controlando o termostato. A uma temperatura de , a tira se encurvou, adquirindo um raio de curvatura , e a extremidade se deslocou de uma distância vertical . Calcule e , sabendo que o coeficiente de dilatação linear do latão é e o do aço é .
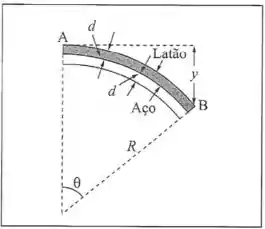
Passo 1
Vamos começar algumas relações geométricas no desenho:
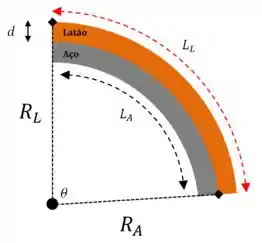
Primeiro vamos observar que a diferença entre os raios é a espessura de uma tira:
E como as duas tiras compreendem o mesmo ângulo, podemos dizer que:
Então:
Nosso objetivo é calcular o maior raio (, então vamos substituir:
E isolar:
Passo 2
Beleza, então precisamos calcular a razão entre os dois comprimentos finais do latão e do aço para encontrar .
As duas tiras tem o mesmo comprimento inicial , então:
A razão é:
Então o raio é:
Passo 3
Ainda falta calcular o deslocamento vertical da extremidade .
Vamos começar calculando o ângulo . Podemos aproveitar uma das relações que escrevemos antes:
Com isso podemos completar nosso desenho:
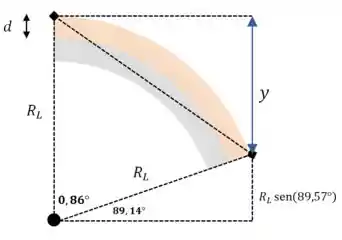
Resposta
O raio é e o deslocamento vertical é .