Duas fontes sonoras e oscilam em fase com a frequência de , no ar, emitindo ondas esféricas; a distância é de . Considere o plano perpendicular a que passa pelo terço do segmento que passa pelo terço do segmento : . Ache as distâncias do ponto associadas aos dois primeiros mínimos e aos dois primeiros máximos de interferência sobre esse plano.
Você poderá utilizar a aproximação: ; a velocidade do som no ar é de . Se as ondas emitidas por e têm a mesma amplitude, qual é a razão da intensidade sonora dos máximos à dos mínimos?

Passo 1
A interferência das duas ondas é causada pela diferença de caminho até certo ponto no plano. Vamos fazer um desenho para ilustrar essa diferença:
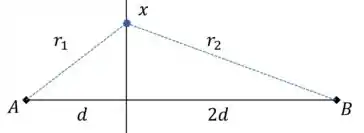
Agora podemos usar o teorema de Pitágoras para calcular e :
Para poder usar a aproximação que foi sugerida no enunciado, vamos escrever da seguinte forma:
Como , podemos reescrever como:
Beleza, já sabemos o caminho que cada onda faz até o ponto em .
Passo 2
Para que ocorra um máximo de interferência, a diferença de caminho deve ser algum múltiplo inteiro de um comprimento de onda:
E já que o enunciado deu a frequência, e não o comprimento de onda, vamos reescrever usando :
Passo 3
Substituindo os valores numéricos (sabendo que ):
Essa expressão só faz sentido enquanto a raiz é positiva. Vamos mostrar que o menor valor de acontece quando :
Esse é o maior valor possível para (do contrário teremos uma raiz negativa), e corresponde a um máximo na origem.
O próximo máximo acontece para :
E o máximo seguinte ocorre em :
Agora vamos procurar os mínimos.
Passo 4
Para que ocorra um mínimo de interferência, a diferença de caminho deve satisfazer a seguinte relação:
E vamos reescrever com :
Passo 5
Agora vamos substituir os valores numéricos:
Então o primeiro mínimo acontece para :
E o segundo para :
Passo 6
Imagine que duas ondas de intensidades e se combinam para formar uma onda de intensidade .
Podemos encontrar a intensidade resultante se soubermos a diferença de fase entre as duas:
Para a intereferência construtiva, a diferença de fase deve ser de uma “volta completa”, ou seja:
E para interferência destrutiva, a diferença de fase deve ser de “meia volta”, então:
Então a razão entre as duas intensidades é:
E a razão entre as duas intensidades pode ser encontrada usando a seguinte fórmula:
Como , podemos aproximar as distância percorridas por:
Então:
Então:
Resposta
Os dois primeiros mínimos ocorrem em e . Os dois primeiros máximos ocorrem em e , além do máximo na origem.
.