Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 25.Exercícios e Problemas - Ex. 24
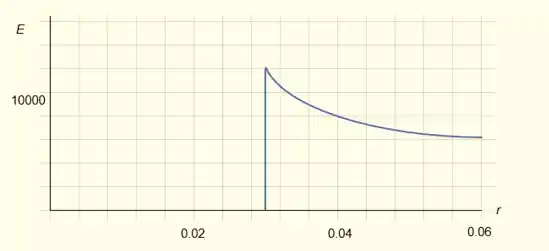
A Fig. mostra uma seção de um tubo longo, de metal, de parede finas, com raio cm e carga por unidade de comprimento. Determine o módulo E do campo elétrico a uma distância radial (a) e (b) . (c) Faça um gráfico de E em função de r para .
Passo 1
Bora lá galera, tudo bom?
Vamos juntos resolver mais um exercício!
Usando o conceito de campo elétrico de uma superfície gaussiana cilíndrica, podemos obter o valor do campo elétrico nas distâncias radiais dadas para a carga encerrada.
O campo elétrico de uma superfície gaussiana cilíndrica,
Para , teremos que:
Imaginamos uma superfície gaussiana cilíndrica A de raio e comprimento unitário concêntrico com o tubo de metal.
Logo para:
Assim, a partir do valor da carga incluída neste caso e na equação (1), obtemos:
Tranquilo?
Passo 2
Para
Para, o campo elétrico, neste caso, é dado usando os dados fornecidos na equação da seguinte forma:
Substituindo os valores:
Passo 3
Hora do gráfico!
O gráfico de é mostrado abaixo:
Aqui, o valor máximo do campo elétrico usando os dados fornecidos na equação é dado como:
Substituindo os valores:
Prontinho!
Te vejo na próxima questão!
Resposta
a)
b)
c)
