Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.1 - Ex. 3
Um trabalhador de um armazém empurra uma caixa ao longo de um piso como indicado na figura abaixo, aplicando uma força de de cima para baixo, formando um ângulo de abaixo da horizontal. Ache os componentes horizontais e verticais da força.
Passo 1
Fala galera, tudo bem? Vou ajudar você nesse exercício, vamos lá?
Esse é um problema de decomposição vetorial. Mas como eu sei isso?
Além de dizer no enunciado, temos uma força sendo aplicada em uma direção, digamos, não usual. Ou seja, ela não está na vertical ou na horizontal. Daí temos que a força se divide em suas componentes, e são essas componentes eu a gente precisa encontrar.
Beleza?
A ideia aqui é fazer um esboço do desenho, incluindo um sistema de eixos ( e ) que seja conveniente pra gente (que tenhamos um triângulo com a força e as componentes) e que inclua também o ângulo de inclinação.
Construído esse triângulo, a gente vai usar as funções seno e cosseno pra deixar as componentes em função do módulo e do ângulo
Mas calma que vou ajudar você.
Vamos começar?
Passo 2
Para ficar mais fácil de ver a decomposição vetorial, vamos fazer um esboço da situação: vou colocar meu eixo horizontal ao longo da linha pontilhada e o eixo vertical ao longo do lado esquerdo a caixa, de modo que a origem desse sistema esteja na ponta da flecha. Saca só como vai ficar:
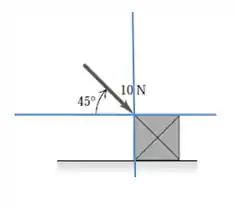Agora vamos decompor esse vetor aí. Pra fazer isso a gente vai precisar usar a imaginação, mas só um pouquinho: o vetor força (esse com a fecha) vai ser nossa diagonal, ou melhor, nossa hipotenusa, e as componentes vertical e horizontal serão os lados do triângulo.
Vou desenhar as componentes em vermelho, olha só:
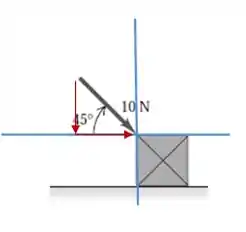
Feito! Nota que a componente vertical é negativa, e isso se dá pela orientação do vetor em cinza, que é o vetor força. O ângulo de é o ângulo que vamos usar como referência para achar as componentes.
O lado oposto a esse ângulo é a nossa componente vertical, e vou chamar ela de . Já o lado queforma o ângulo, junto com o vetor cinza, é nosso cateto adjacente, e é também nossa componente horizontal.
Vou chama ela de . Usando só os eixos e os vetores temos esse desenho:
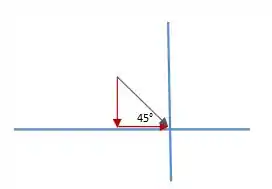
Como o ângulo que temos é entre a força (representada pelo vetor roxo no desenho) e a componente horizontal então o cateto adjacente vai ser e o cateto oposto vai ser . E a hipotenusa? É e vale , certo? Beleza! Agora basta usar as funções seno e cosseno! Bora lá?
Passo 3
A componente vertical vai estar associada com a função seno:
E a componente horizontal vai estar associada com a função cossseno:
Mas como a componente vertical é na direção negativa do eixo precisamos colocar um sinal indicativo de :
E aí! entendeu tudo? Responde Aí!
