Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.1 - Ex. 6
Duas forças e , atuam sobre um ponto. O módulo de é igual a , e sua direção forma um ângulo de acima do eixo no segundo quadrante. O módulo de é igual a , e sua direção forma um ângulo de abaixo do eixo no terceiro quadrante.
Quais são as componentes e da força resultante?
Qual o módulo da força resultante?
Passo 1
Oi, galerinha! Tudo bom?
Nós temos duas forças descritas na questão, então vamos fazer um esquema para entender melhor:
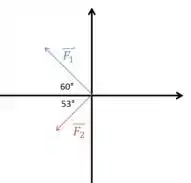
Um vetor qualquer pode ser decomposto da seguinte forma:
Onde é a intensidade do vetor e é o ângulo formado com o eixo no sentido anti-horário.
Bora aplicar!
Passo 2
- Para a força temos que sua intensidade é de e sua direção forma um ângulo com o eixo , mas no segundo quadrante. Mas por definição, usamos sempre em relação ao primeiro quadrante. Sendo assim, em relação ao primeiro quadrante esse ângulo é
- E o módulo? Ah, pra descobrir o módulo temos que lembrar da fórmula do módulo de um vetor :
Assim a decomposição do vetor é:
Para a força temos que sua intensidade é de e sua direção forma um ângulo abaixo do eixo , no terceiro quadrante. Mas por definição, usamos sempre em relação ao primeiro quadrante. Sendo assim, em relação ao primeiro quadrante esse ângulo é
Assim a decomposição do vetor é:
E a força resultante vai ser a soma das duas outras forças. Lembrando que a soma de vetores é feita somando-se componente a componente, temos:
Então a componente da força resultante é e a componente vertical é
Tranquilo até aqui?
Passo 3
Como no passo anterior já determinamos as componentes e da força resultante, fico tranquilo descobrir o módulo, basta substituir:
E aí! entendeu tudo? Responde Aí!
