Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.1 - Ex. 1
Duas forças possuem módulo . Qual é o ângulo entre dois vetores quando a soma vetorial possui o módulo igual a a)? b)? c) zero? Faça um desenho dos três vetores em cada caso.
Passo 1
Fala aí! como vai?
Nesse problema temos duas forças de modulo e nosso objetivo é obter o ângulo entre essas forças de modo que a força resultante seja , e .
Tem ideia de como fazemos isso?
Podemos determinar o módulo da soma vetorial de dois vetores quaisquer que chamaremos de e , podemos usar a lei dos cossenos que é dada por:
O ângulo formado entre dois vetores é o menor ângulo que pode existir entre e . O exercício nos diz que e tem o mesmo módulo (que por convenção chamaremos de )
Bora lá!
Passo 2
Na letra a do exercício, nós temos que a resultante é dada por , aplicando na lei dos cossenos, teremos:
Sendo que ,
A representação gráfica fica algo como:
Tranquilo até aqui?
Passo 3
O segundo caso do exercício é quando a resultante é , aplicando na lei dos cossenos, teremos:
Sendo que ,
A representação gráfica fica algo como:
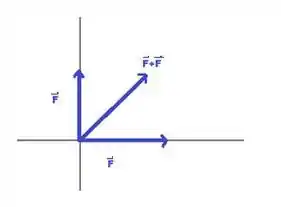
Bacana, não é?
Passo 4
A ultima opção é quando a resultante é nula, , aplicando na lei dos cossenos, teremos:
Sendo que ,
A representação gráfica fica algo como:
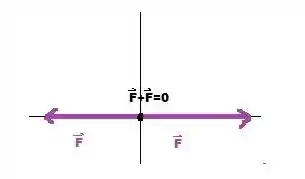
Nesse caso, os vetores são antiparalelos para formar esse ângulo.
E aí! o que achou? Responde Aí!