Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.1 - Ex. 2
Em vez de usar os eixos e da figura para analisar a situação do Exemplo , use um sistema de eixos girados de no sentido anti-horário, de modo que o eixo seja paralelo à força de
Para esses eixos, ache os componentes e da força resultante que atua sobre a partícula.
Partindo dos componentes calculdos em , calcule o módulo, a direção e o sentido da força resultante. Compare seus resultados com o Exemplo
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que rotacionar o sistema em (anti-horario) de tal forma que a força seja paralela a .
A partir daí queremos calcular as componentes da força resultante além do módulo, direção e sentido.
Parece complicado?
Vamos relembrar qual é a figura que o problema fala:
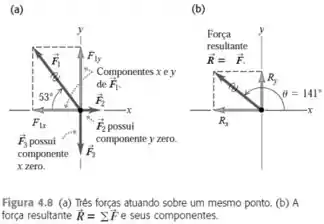
Os novos eixos depois de feita a rotação estão em azul:
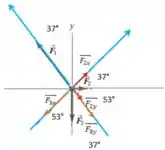
Nessa nova configuração o vetor ficou na direção do eixo :
Bora lá!
Passo 2
As componentes e da força estão em vermelho. Ele vai ter um ângulo, a partir da origem, de , sua componente horizontal é positiva e a vertical é negativa.
As componentes da força estão desenhadas em laranja. A partir da nova origem, ela vai fazer um ângulo de . Suas duas componentes serão negativas.
Considerando isso, usaremos a fórmula para considerar as decomposições dos eixos e já realizaremos as somas de Sendo assim, as componentes da força resultante vão ser:
Assim o vetor resultante é:
Tranquilo até aqui?
Passo 3
O módulo de um vetor é dado por:
Assim o módulo do vetor é:
E para determinar a direção e sentido, precisamos saber qual ângulo em relação à origem ele faz. Lembrando que o ângulo pode ser dado pela fórmula
Podemos substituir os valores das componentes:
Então o módulo da força será e o vetor faz um ângulo de com a nova origem de coordenadas.
Show?
Passo 4
E em comparação com o exemplo? Dá uma espiadinha no exemplo do livro! O módulo não é o mesmo? É sim! Isso porque não importa o sistema de coordenadas, o módulo da força resultante sempre vai ser o mesmo!
E quanto ao ângulo? O ângulo do exemplo é e o nosso resultado foi de . Uma diferença de exatos ! Exatamente a rotação feita lá no começo!
Beleza? O que achou? Responde Aí!
