Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 3.Exercícios e Problemas - Ex. 16
Uma transformação de coordenadas é gerada pela matriz:
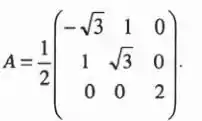
Trata-se de transformação própria ou imprópria?
Passo 1
Meus lindos e minhas lindas, para saber se trata de uma transformação própria ou imprópria precisamos calcular o determinante da matriz.
Logo:
Mãos a obra!
Repetindo as colunas 1 e 2 e multiplicando todos os termos da matriz por , calcularemos o determinante da matriz A:
Vamos por etapa para não confundir vocês:
Com isso:
Portanto, trata-se de uma transformação imprópria.
Resposta
Imprópria.
Exercícios de Livros Relacionados
Dois vetores são dados por a → = 4,0m i ^ - 3,0m j ̂ +1,0m k ^ e b → = - 1,0m i ^ +1,0m j ^ + 4,0m k̂ . Determine, em termos de vetores unitários, (a) a → +b⃗ ; (b) a → -b⃗ ; (c) um terceiro vetor, c⃗
Você deve executar quatro deslocamentos sucessivos na superfície plana num deserto, começando na origem de um sistema de coordenadas x y e terminando nas coordenadas ( - 140m ,30m ) . As componentes d
Uma pessoa deseja chegar a um ponto que está a 3,40k m de sua localização atual, em uma direção 35,0 ° ao norte do leste. As ruas por onde pode passar são todas na direção norte-sul ou na direção lest
Para os vetores a → = 3,0m i ^ + ( 4,0m ) j ^ e b → = 5,0m i ^ + ( - 2,0m ) j ^ , determine a → + b → (a) em termos de vetores unitários e em termos (b) do módulo e (c) do ângulo (em relação a i ^ ).
Uma pessoa caminha da seguinte forma: 3,1k m para o norte, 2,4k m para o oeste e 5,2k m para o sul. (a) Desenhe o diagrama vetorial que representa este movimento. (b) Que distância e (c) em que direçã