Uma pessoa caminha da seguinte forma: para o norte, para o oeste e para o sul. (a) Desenhe o diagrama vetorial que representa este movimento. (b) Que distância e (c) em que direção voaria um pássaro em linha reta do mesmo ponto de partida ao mesmo ponto de chegada?
Passo 1
(a)Vamos iniciar essa questão fazendo o diagrama vetorial que representa o movimento:
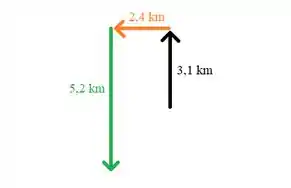
Para fazer este diagrama seguimos o caminho que a pessoa da questão fez.
Passo 2
Para saber a distância que o pássaro teria que voar partindo da origem e indo até o ponto final que a pessoa chegou, precisamos encontrar o vetor resultante do diagrama vetorial feito acima. Para isso faremos o somatório dos vetores que compõem o deslocamento.
Estabelecendo um plano cartesiano:
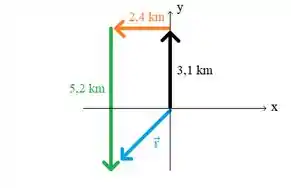
E escrevendo os vetores em componentes:
Fazendo a soma dos vetores:
Beleza?!
Passo 3
(b)Com o vetor resultante calculado em função das componentes, podemos calcular o módulo do vetor para encontrar a distância percorrida pelo pássaro:
Passo 4
(c)Para determinar a direção faremos um triângulo retângulo para facilitar a visualização da trigonometria que será aplicada para determinar o ângulo do vetor:
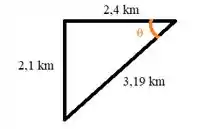
Aplicando a definição de cosseno:
Isolando o :
Logo, a direção que o pássaro terá que voar é de oeste para sul.
Resposta
-
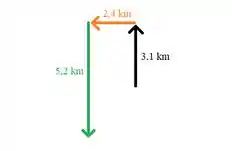
- de oeste para sul