Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.6 - Ex. 12
Para os vetores e , determine (a) em termos de vetores unitários e em termos (b) do módulo e (c) do ângulo (em relação a ). Determine (d) em termos de vetores unitários e em termos (e) do módulo e (f) do ângulo.
Passo 1
Vamos iniciar esta questão fazendo o somatório vetorial direto, pois o problema já nos deu os vetores em notação de componentes. Para isso, faremos:
Em seguida, com o vetor resultando escrito em função das componentes, vamos aplicar a definição de módulo de vetor:
E, por fim, usaremos a trigonometria para determinar o ângulo que o faz com o semieixo positivo.
Passo 2
Com os valores das componentes dos vetores dados, podemos fazer o somatório vetorial definido no passo anterior:
Substituindo os valores:
Passo 3
Agora, aplicando a definição do módulo de vetor, também anunciado no passo :
Passo 4
Para determinar o ângulo que o vetor faz com semieixo positivo vamos representa-lo no plano cartesiano e vamos definir um triângulo retângulo formado com as componentes e o vetor principal:
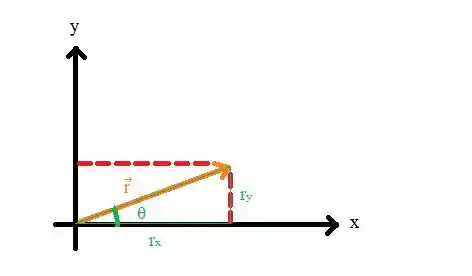
Então, aplicando a definição de cosseno:
Substituindo os valores:
Isolando o :
Passo 5
Agora, com os valores das componentes dos vetores dados, podemos fazer o somatório vetorial definido no passo inicial:
Substituindo os valores:
Passo 6
Agora, aplicando a definição do módulo de vetor, também anunciado no passo :
Passo 7
Para determinar o ângulo que o vetor faz com semieixo positivo vamos fazer de maneira análoga ao que fizemos no passo :
Então, aplicando a definição de cosseno:
Substituindo os valores:
Isolando o :
Resposta
- ;
- ;
- ;
- ;
- .