Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 90
Um trem partiu do repouso com aceleração constante. Em um certo instante, estava se movendo a ; adiante, estava se movendo a calcule:
(a) a aceleração,
(b) o tempo necessário para percorrer os mencionados;
(c) o tempo necessário para atingir a velocidade de ;
(d) a distância percorrida desde o repouso até o instante que o trem atingiu a velocidade de ;
(e) Desenhe os gráficos de em função de e de em função de, de até o instante em que o trem atingiu a velocidade de .
Passo 1
Este é um problema de MRUV, pois o enunciado diz que o trem possui aceleração constante. Para essa questão, em especial, precisamos ter em mente:
(equação de Torricelli)
E, além disso, lembrar que , ou seja, para o MRUV a aceleração média e a aceleração instantânea são iguais.
Passo 2
Para determinar aceleração utilizaremos a equação de Torricelli entre o instante que o trem está se movimentando a e o instante em que se locomove a , pois aqui sabemos o deslocamento entre esses dois pontos. Então:
Isolando :
Passo 3
Para determinar o tempo necessário para percorrer os mencionados, utilizaremos a fórmula da aceleração média entre os mesmo instantes do passo anterior:
Substituindo os valores e isolanto o , temos:
Passo 4
Também utilizaremos a fórmula da aceleração média para determinar o tempo necessário para atingir a velocidade de , porém, agora vamos usar o instante inicial que o trem parte do repouso e o instante em que ele atinge :
Substituindo os valores e isolando :
Passo 5
Para determinar a distância percorrida desde o repouso até o instante que o trem atingiu a velocidade de , utilizaremos a equação de Torricelli:
Passo 6
Os gráficos de em função de e de em função de , de até o instante em que o trem atingiu a velocidade de são:
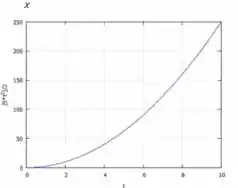
Resposta
- ;
- ;
- ;
- ;
-
