Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 14

Três cargas puntiformes positivas iguais (cada uma carga + q ) estão fixas nos vértices de um triângulo equilátero que tem lados com comprimento a . A origem está no ponto médio de um dos lados do triângulo, o centro do triângulo está no eixo x em x = x 1 e o vértice oposto à origem está no eixo x em x = x 2 . (a) Expresse x 1 e x 2 em termos de a . (b) Escreva uma expressão para o campo elétrico no eixo x a uma distância x da origem no intervalo 0 < x < x 2 . (c) Mostre que a expressão que você obteve em (b) fornece os resultados esperados para x = 0 e x = x 1 .

Passo 1

O esquema abaixo resume o que foi dito no enunciado.

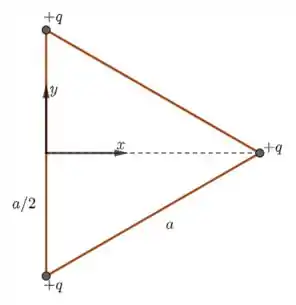
Passo 2

  1. Aplicando Pitágoras, vemos que

    2. x 2 = a 2 - a / 2 2 x 2 = 3 a 2

    Da geometria, sabemos que o centro de um triângulo equilátero está a uma distância 1 / 3 do lado. Sendo assim,

    x 1 = 1 3 x 2 x 1 = 3 a 6

    Passo 3

  2. Temos que, para um x qualquer

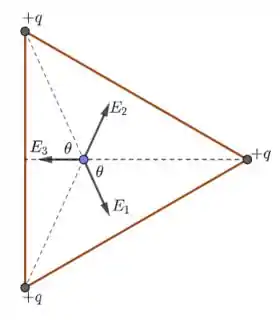
  • Note que a resultante entre E 1 e E 2 aponta na direção do eixo x (para a direita). Temos que

E 1 = E 2 = k q x 2 + a / 2 2 = 4 k q 4 x 2 + a 2

Além disso,

cos ⁡ θ = x x 2 + a / 2 2 = 2 x 4 x 2 + a 2

Assim, a resultante entre E 1 e E 2 , E 12 , é:

E 12 = E 1 cos ⁡ θ + E 2 cos ⁡ θ = 2 E 1 cos ⁡ θ E 12 = 2 4 k q 4 x 2 + a 2 2 x 4 x 2 + a 2 E 12 = 16 k q x 4 x 2 + a 2 3 / 2

Também temos que

E 3 = k q x 2 - x 2 = k q 3 2 a - x 2

Dessa forma, o campo elétrico resultante em um ponto x qualquer aponta na direção horizontal e tem módulo:

E = E 12 - E 3 E x = k q 16 x 4 x 2 + a 2 3 / 2 - 1 3 2 a - x 2

Passo 3

  • Fazendo x = 0 , temos

    • E 0 = k q ⋅ 0 - 1 3 2 a 2 = - 4 k q 3 a 2

    (o sinal negativo indica que aponta no sentido contrário ao do eixo x )

    Fazendo x = x 2 , temos

    E 3 6 a = k q 16 ⋅ 3 6 4 ⋅ 1 12 a 2 + a 2 3 / 2 - 1 3 2 a - 3 6 a 2 E 3 6 a = k q 3 a 2 - 3 a 2 = 0

    Ou seja, o campo em x = x 2 é zero.

    Resposta

    1. 3 6 a e 3 3 a
    2. k q 16 x 4 x 2 + a 2 3 / 2 - 1 3 2 a - x 2
    3. - 4 k q / 3 a 2 e zero
    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    PROTEÇÃO CONTRA RADIAÇÃO CÓSMICA. Um dos perigos para os seres humanos no espaço é a radiação cósmica: partículas carregadas com alta energia emitidas pelo Sol. Durante uma erupção solar, a intensidad
    Uma carga puntiforme igual a - 3,00n C está sobre o eixo x no ponto x = 1,20m . Uma segunda carga puntiforme Q está sobre o eixo x no ponto x = - 0,600m . Determine o módulo e o sinal de Q de modo que
    Campo elétrico de axônios. Um sinal nervoso é transmitido através de um neurônio quando um excesso de íons de N a + subitamente entra no axônio, uma parte longa e cilíndrica do neurônio. Axônios possu
    Se dois elétrons estão cada um a uma distância igual a 1,50 × 10 - 10m de um próton (Figura E21.45), encontre o módulo, a direção e o sentido da força elétrica resultante que eles irão exercer sobre o
    Duas partículas cujas cargas são q 1 = 0,500n C e q 2 = 8,0n C estão separadas por uma distância de 1,2m . Em que ponto entre as cargas o campo elétrico resultante das duas cargas é igual a zero?