Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 55
Um condutor em forma de anel com raio a=2,5 cm possui uma carga positiva Q=+0,125 nC uniformemente distribuída ao longo do anel, como indica a figura 21.24. O centro do anel está na origem do sistema de coordenadas.
(a) Qual o campo elétrico (módulo, direção e sentido) no ponto situado em .
(b) Uma carga puntiforme está no ponto descrito na parte (a). Determine o módulo, direção e sentido da força exercida pela carga sobre o anel.
Passo 1
(a) A fórmula para o campo elpetrico de anel é tabelada e vale:
Onde é o raio do anel, que vale , e , que é a distância do centro do anel ao ponto . Já que foi dito que o anel está na mesma configuração da figura 21.24:
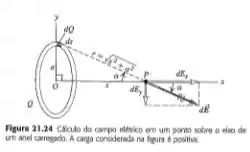
Dessa forma, podemos ver que o campo elétrico resultante sobre estará apenas no eixo , só pensar na simetria do anel, que vai cancelar todas as outras componentes!
Nossa fórmula para o campo fica:
Onde :
Fazendo as contas, chegamos a:
Passo 2
(b) Agora, temos que saber a força elétrica exercida pela carga SOBRE o anel.
Temos que pensar o seguinte: pela terceira lei de Newton, a força que o anel exercer sobre a carga gera uma força contrária e de mesmo módulo como reação. Hmmmm, mas por quê isso vai ser importante? Bom, porque nós temos o campo elétrico produzido pelo anel, então podemos calcular a força sobre a carga dessa forma:
Só que queremos a força sobre o anel e, como já vimos, ela será a reação a , ou seja, com mesmo módulo, mas sentido oposto:
Dessa forma:
Como já calculamos e :
Resposta
(a)
(b)