Denomina-se coroa anular um disco fino de raio externo com um buraco circular concêntrico de raio interno (figura 21.51). Uma coroa anular possui uma densidade superficial de carga sobre sua superfície.
(a) Determine a carga total sobre a coroa anular.
(b) A coroa anular está sobre o plano com seu centro na origem. Para um ponto arbitrário sobre o eixo (eixo de simetria da coroa anular), determine o módulo, a direção e o sentido do campo elétrico . Considere todos os pontos acima e abaixo do plano da coroa anular da figura 21.51.
(c) Mostre que, para os pontos sobre o eixo suficientemente próximos da origem, o módulo do campo elétrico é aproximadamente proporcional à distância entre o centro da coroa e o ponto considerado. Qual é a distância que pode ser considerada suficientemente próxima?
(d) Uma partícula puntiforme com massa e carga pode se mover livremente sobre o eixo (mas não pode sair desse eixo). A partícula é inicialmente colocada sobre o ponto e, a seguir, liberada. Determine a frequência das oscilações da partícula.
Passo 1
(a) Bom, queremos calcular toda a carga presente na coroa, certo? Sabemos que podemos calcular pela densidade de cargas, já que a densidade superficial é:
Nós sabemos a densidade , pois foi dito que ela é conhecida no enunciado. Mas como vamos achar essa área, então? Nós temos a área de uma coroa anular, que, vendo de cima, é dessa forma:
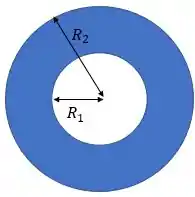
Para calcular a área, podemos fazer a área do círculo de raio e diminuir a área do furo, que seria do círculo de raio :
Colocando em evidência:
Substituindo essa expressão ali em cima:
Essa é a carga total da coroa.
Passo 2
(b) Nós temos uma situação mais ou menos assim:
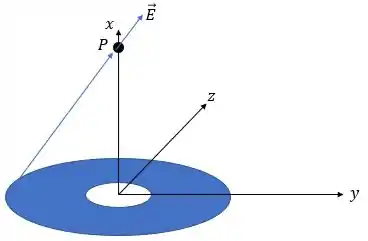
Onde, por simetria, a gente sabe que a única componente desse campo elétrico que vai sobrar é a componente em . Todas as outras, terá um ponto na coroa que vai cancelar a componente.
Mas vamos pensar uma coisinha: se a coroa não tivesse esse furo? Ela seria um disco, certo? E sabemos que o campo elétrico produzido por um disco em um ponto no eixo do seu centro distante de um valor seria:
Como temos que considerar todos os pontos acima e abaixo do disco, colocamos o fator para dar conta disso. Pensa comigo: o campo elétrico em um ponto seria numa direção, só o campo num ponto seria na direção oposta, mas igual em módulo. Pois a diferença seria apenas a direção do vetor:
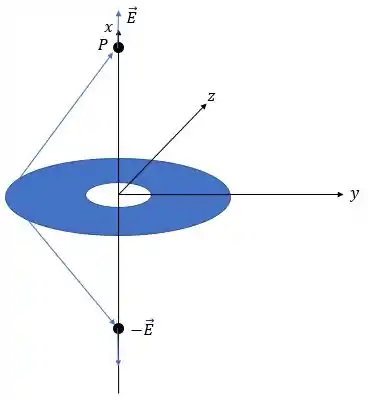
Então, a diferença seria apenas o sinal, certo? Para isso resolve nosso problema, pois se , será e, se , , o que mudará o sentido do vetor! Dessa forma, os resultados sempre batem! Show?
Maasss nós temos o furo ali, então temos que tirar o campo elétrico que esse furo produziria! Esse furo tem o formato de um disco de raio , então o campo elétrico produzido por ele seria:
A única mudança é no raio. Então, da mesma forma que tiramos a área do furo para resolver a letra (a), aqui, vamos tirar esse campo que o furo produziria! Nosso campo final será o campo do disco inteiro menos o campo do furo:
Podemos colocar em evidência:
Assim, podemos arrumar o parêntese ali:
Fazendo o :
Vamos só trocar a ordem para ficar mais bonitinho:
Prontinho! Esse é o campo elétrico da coroa para qualquer ponto no eixo .
Passo 3
(c) Ok, vamos com calma, queremos analisar um muito próximo, então vamos olhar para onde o aparece na fórmula do campo elétrico:
Bom, se a gente colocar em evidência na primeira raiz e na segunda raiz:
Se você fizer essa multiplicação de novo ( e ), vai voltar a ter o que era inicialmente ( e ), então, tudo certo.
Agora, podemos tirar o da primeira raiz e o da segunda raiz:
Por quê o módulo no ? Porque podemos ter valores positivos e negativos dele!
E, arrumando essa divisão, o vai para o numerador:
Agora, se o for pequeno suficiente para que e , aquela soma ali será praticamente igual a , por exemplo: , isso é praticamente , certo? Então, poderíamos dizer que:
Com isso, nosso campo elétrico ficaria:
Colocando em evidência:
Só que, concorda comigo que qualquer número ao quadrado será sempre positivo? Então , não precisamos mais desse módulo! E, assim:
Podemos simplificar o :
Esse seria o campo elétrico se fosse suficientemente próximo de forma que e .
Passo 4
(d) Repare que se , ele já entra no critério para ser suficientemente próximo () e nosso campo passa a ser:
A força elétrica que será exercida sobre a carga de será:
Substituindo:
Se temos uma oscilação por conta dessa força elétrica, podemos dizer que ela faz o papel de uma força elástica, logo, ela simula um movimento harmônico, com uma força do estilo:
Onde, por comparação com as duas fórmulas de :
Agora, vamos ter que relembrar mais uma coisinha lá do movimento harmônico: a fórmula para a frequência de oscilação:
Opa, sabemos que a massa da partícula é e sabemos o também, vamos substituir:
Então, essa será a frequência de oscilação da partícula, caso ela esteja suficientemente próxima da origem!
Resposta
(a)
(b)
(c); e .
(d)