Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 45
Três finas cascas cilíndricas condutoras, longas e concêntricas, têm raios de , e . O espaço entre as cascas é preenchido com ar. A casca mais interna está conectada à casca mais externa por um fio condutor em uma das extremidades. Determine a capacitância por unidade de comprimento desta configuração.
Passo 1
POW! O problema nos disse o seguinte... Temos três cilindros todos concêntricos...
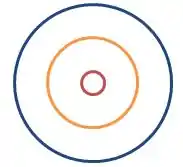
Só que a gente liga o cilindro mais externo ao interno...
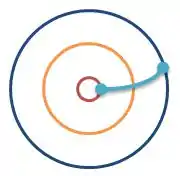
Cara, os dois cilindros podem ser considerado como um capacitor, só que aqui temos dois cilindros unidos e um cilindro interno, como se tivéssemos dois capacitores normais unidos de modo que quando ligamos a casca azul numa tensão e a laranja em outra...
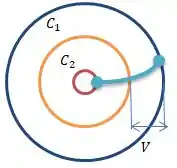
E aí, como a azul está ligada na vermelha, a mesma diferença de potencial surge entre a vermelha e a laranja...
Consegue visualizar? O que eu estou tentado te falar é que os espaços cilíndricos se comportam de modo semelhante, ou seja, como se as capacitâncias deles estivessem em paralelo, ta ligado?
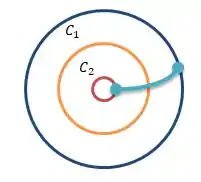
Passo 2
Tá, pela teoria, conhecemos as capacitâncias e ...
A capacitância equivalente então será...
A capacitância do conjunto por unidade de comprimento então será...
Como ...
Ou ainda...