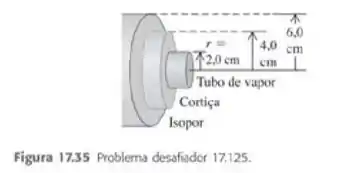
Um tubo de vapor d’água com raio igual a transportando vapor a é revestido por um involucro cilíndrico com um raio interno de e um raio externo de , e feito com um tipo de cortiça de condutividade térmica igual a . Esse cilindro, por sua vez, é revestido por outro involucro cilíndrico com uma camada de isopor com condutividade térmica igual a com um raio interno de e um raio externo igual a (Figura17.35). A superfície externa do isopor está a uma temperatura de . a) A um raio de , qual é a temperatura no local onde as duas superfícies se juntam? b) Qual é a taxa total de transferência de calor a partir de uma extensão de do tubo? (Sugestão: Use a expressão deduzida na parte (c) do Problema desafiador 17.122.)

Usando a equação deduzida no problema 122, que é a equação para um cilindro com duas camadas de raios diferentes:

A ultima igualdade do passo 1 fica:

Simplificando:

Agora isolamos a variação de temperatura através do isopor:

E substituímos ele na primeira relação do passo 1 que definimos:

Para achar a variação na cortiça:

A variação de temperatura do processo todo é (de dentro do tubo até a parte externa):

Substituindo esse valor junto com as condutividades térmicas de cada material dados pelo enunciado:

E como temos a temperatura dentro do vapor dentro do cano que é a temperatura inicial, e a variação dentro da cortiça, podemos achar a temperatura final para a cortiça que será exatamente a temperatura entre as duas superfícies:

b) E como a transferência de calor do processo todo é igual à de cada material, porque eles estão em série, podemos usar o para calcularmos a taxa de transferência no tubo todo: