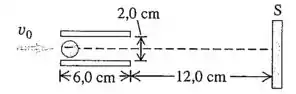
Os tubos de raios catódicos (CRT, do inglês cathode-ray tubes) são geralmente encontrados em osciloscópios e monitores de computador. Na figura abaixo, um elétron com velocidade inicial de é projetado ao longo do eixo até o meio da trajetória entre as placas de reflexão de um tubo de raios catódicos. O campo elétrico uniforme entre as placas possui módulo e está orientado de baixo para cima.

a)Qual é a força (módulo, direção e sentido) que atua sobre o elétron quando ele está entre as placas?

b)Qual é a aceleração do elétron (módulo, direção e sentido) quando ele sofre a ação da força obtida no item (a)?

c)Qual é a distância abaixo do eixo percorrido pelo elétron, quando ele atinge o final das placas?

d)Qual é o ângulo dele em relação ao eixo quando se move para deixar as placas

e)A que distância abaixo do eixo ele atingirá a tela fluorescente?

letra b)

Pela 2° lei de Newton podemos escrever:

letra c)

Queremos saber a variação da posição do elétron no eixo y.

Lembrando que ele está se movendo tanto no eixo x quanto no eixo y.

O que isso significa??????

LANÇAMENTO OBLÍQUO!!!

Podemos tratar esse tipo de questão como uma questão de lançamento oblíquo.

No eixo x:

A partir da fórmula da posição temos:

No eixo y:

Queremos e sabemos que

letra d)

Para achar o ângulo, podemos relacionar as componentes da velocidade como na figura abaixo.

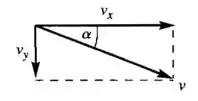
Pelo desenho vemos que podemos relacionar o ângulo com as componentes da velocidade a partir da relação:

Precisamos agora achar e :

Substituindo na expressão:

letra e)

Como no item (c) usaremos

LANÇAMENTO OBLÍQUO!!!

No eixo x:

A partir da fórmula da posição temos:

No eixo y:

A partir do item (d):

Queremos e sabemos que

Quando está entre as placas, o elétron se move

Quando sai das placas, o elétron se move