Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 2.Exercícios e Problemas - Ex. 12
Utilize a transformação dada pela Equação 3.52 para calcular as componentes do vetor a’ da Figura 3.5 no sistema de coordenadas .
Passo 1
Oi pessoas, tudo certo com vocês? Espero que sim 😊. Nessa questão vamos utilizar essa equação:
Não se assuste, podemos resumir ela fazendo uma simples multiplicação entre matrizes. Assim, podemos simplificar dessa maneira,
Passo 2
Observação importante! Essa equação foi deduzida a parti dessa imagem:
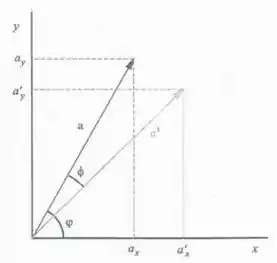
Ou seja, o ângulo que vamos utilizar na fórmula é . Atenção!
Como o vetor a é igual a
Temos que,
Para teremos:
Resposta
Exercícios de Livros Relacionados
Um tatu assustado pula verticalmente para cima, subindo 0,544m nos primeiros 0,200s . (a) Qual é a velocidade do animal ao deixar o solo? (b) Qual é a velocidade na altura de 0,544m ? (c) Qual é a alt
Um parafuso se desprende de uma ponte em construção e cai 90 m até chegar ao solo. (a) Em quanto tempo o parafuso percorre os últimos 20% da queda? Qual é a velocidade (b) quando começam os últimos 20
Uma pedra é deixada cair em um rio a partir de uma ponte situada 43,9m acima da água. Outra pedra é atirada verticalmente para baixo 1,0s após a primeira ter sido deixada cair. As pedras atingem a águ
Um balão de ar quente está subindo a uma taxa de 12m / s e está a 80m acima do solo quando um tripulante deixa cair um pacote. ( a ) Quanto tempo o pacote leva para atingir o solo? ( b ) Com que veloc
Uma bola de argila úmida cai 15,0m até o chão e permanece em contato com o solo por 20,0m s antes de parar completamente. (a) Qual é o módulo de aceleração média da bola durante o tempo de contato com