Verifique se a constante de normalização A0 na função de onda do oscilador harmônico no estado fundamental () 20 0ax x A e− = ((Equação 35-23) é dada por () 1 40 0 A = 2mω h.

Primeiro, vamos ver que se temos tudo elevado ao quadrado, não precisamos desse módulo, pois qualquer número ao quadrado é positivo!! Além disso, vamos tirar o de dentro da integral, por ele ser um termo constante:

Agora, temos que pensar no seguinte: como temos um ali, se pegarmos um número e seu oposto ( e , por exemplo), quando elevarmos ao quadrado teremos o mesmo resultado (, no caso). Aonde quero chegar? Que a mesma coisa que acontece para os números positivos acontece para os negativos nessa função!! Ou seja, temos uma simetria em relação ao eixo . O gráfico dessa função é algo do tipo:

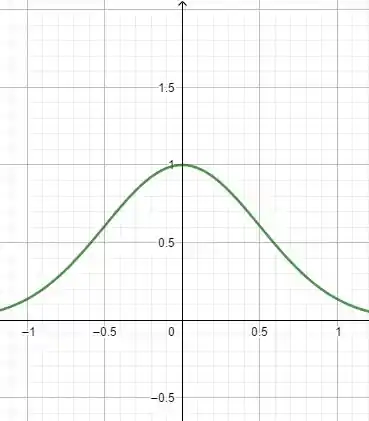
Então, repare na simetria em relação ao . Dessa forma, podemos ver que a área embaixo da curva (sua integral) vai ser igual para e . Assim:

Beleza? Vamos dizer que :

Opa, agora essa é exatamente uma das integrais tabeladas! O resultado é:

Como :

Substituindo isso na expressão que tínhamos:

Simplificando:

Dessa forma:

Agora, temos que lembrar lá do exemplo 35-1, onde tínhamos:

Substituindo esse na expressão para :

Como :

Prontinho!