Enunciado
Física - Tipler - Vol 3- Ed: 6º - Capítulo 34.1 - Ex. 52
(a) Use um programa de planilha ou calculadora gráfica para plotar x2 como uma função do número quântico n para a partícula na caixa descrita no Problema 48 e para valores de n de 1 a 100. Suponha L = 1,00 m para o seu gráfico. Consulte o Problema 51. (b) Comente a importância de quaisquer limites assintóticos que o seu gráfico mostre.
Passo 1
(a) Do problema 51, nós temos que:
E:
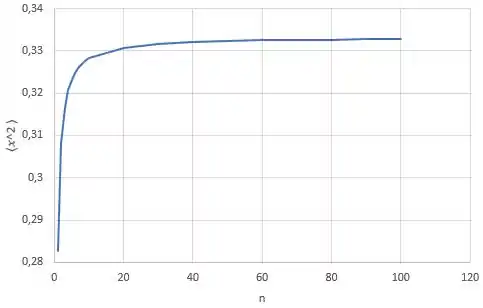
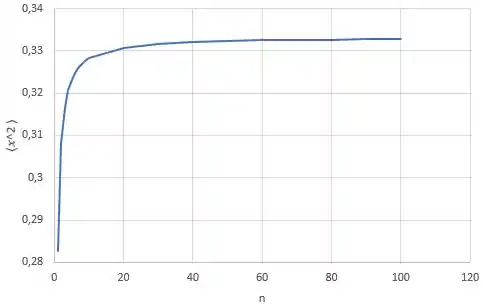
Assumindo , temos que plotar o gráfico de:
O gráfico fica:
Passo 2
(b) Pelo gráfico, a gente percebe que quando tende ao infinito tende a , ou seja, chega um momento em que não muda muito mais, pois está tendendo a , mas nunca chega nesse valor.
Resposta
Exercícios de Livros Relacionados
Uma caixa unidimensional está no eixo x na região de 0 ≤ x ≤ L. Uma partícula nesta caixa está em seu estado fundamental. Calcule a probabilidade de a partícula ser encontrada na região (a) x L21 0
Uma partícula em uma caixa unidimensional com comprimento L está no primeiro estado excitado (n = 2). (A caixa tem uma extremidade na origem e a outra extremidade no eixo x positivo.) (A) Esboço ψ 2 (
Uma partícula de massa m tem uma função de onda dada por ψ x = A e - x a , onde A e a são constantes positivas. (a) Encontre a constante de normalização A. (b) Calcule a probabilidade de encontrar a p