Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 4
Um vetor posição, do primeiro quadrante, tem um componente de e um módulo de . Qual é o valor de seu componente ?
Passo 1
O problema nos fornece o valor da componente e o módulo do vetor posição, que vou chamar de , e nos pede o valor da componente :
Vamos aproveitar que foi fornecido o valor do módulo e utilizar a fórmula para calcular o módulo do vetor:
Passo 2
Como temos os valores de e , a nossa única incógnita é o e podemos isolar na fórmula:
Note que na fórmula aparece um , isso acontece porque o valor de estava elevado ao quadrado, e quando um número é elevado ao quadrado, o resultado é sempre positivo, mesmo que o número seja negativo, então tem a possibilidade de ser negativo ou positivo, por isso o .
Agora, temos que colocar na fórmula os valores de e que foi fornecido, e achamos o valor de .
Passo 3
Agora, temos que analisar se o valor de é positivo ou negativo.
A questão nos diz que o vetor posição, , está no primeiro quadrante. O primeiro quadrante é aquele em que os valores de e são positivos:
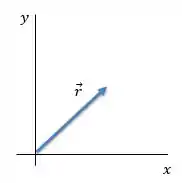
Quando formos decompor o vetor, vamos ver que os valores das componentes e serão positivas porque estarão apontando no sentido dos eixos.
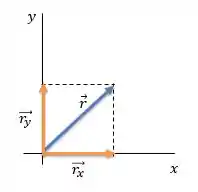
Então, a componente é positiva: