1. O módulo de um vetor pode ter valores diferentes em diferentes sistemas de coordenadas.

O módulo de um vetor é sempre o mesmo, independente do sistema de coordenadas. Isso acontece porque o módulo é o tamanho do vetor e esse tamanho não muda.

O sistema de coordenadas é a maneira com que eu decido descrever o vetor, se eu escolho escrever de uma maneira ou de outra, o tamanho do vetor continua, belezinha?

Então, a letra a é FALSA.

Passo 2

2. A orientação de um vetor pode ser diferente em diferentes sistemas de coordenadas.

A orientação do vetor no espaço é independente de qualquer sistema de coordenadas.

Dá uma olhada aqui nessa imagem:



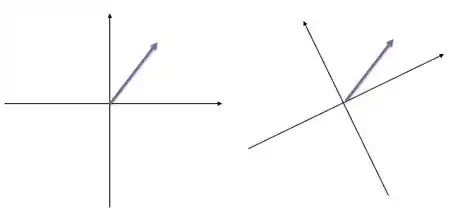
Percebe que são dois sistemas de coordenadas diferentes, que eu posso utilizar para descrever esse vetor, o ângulo que o vetor faz com os eixos em cada sistema é diferente, mas a orientação do vetor NO ESPAÇO é EXATAMENTE a mesma, notou?

Então, a letra b também é FALSA.

Passo 3

3. Os componentes de um vetor podem ser diferentes em diferentes sistemas de coordenadas.

Vamos novamente pegar aquela imagem que usamos para a letra b e representar as componentes do veto em cada um dos sistemas de coordenadas:

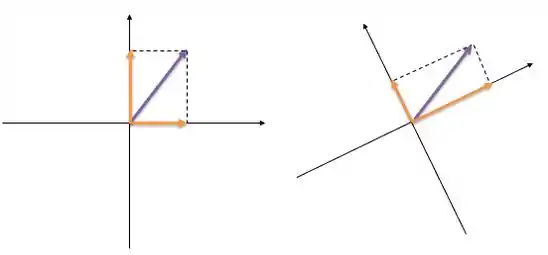
Percebe que as componentes em cada sistema de coordenadas são diferentes? Isso acontece justamente porque o ângulo que o vetor faz com cada sistema de coordenadas é diferente, show?

Então, a letra c é VERDADEIRA, as componentes de um vetor podem ser diferentes em diferentes sistemas de coordenadas.