Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 43c
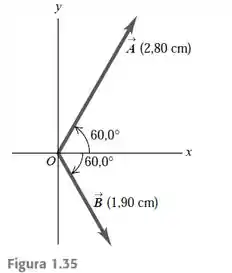
O vetor possui comprimento igual a e está no primeiro quadrante a acima do eixo . O vetor possui comprimento igual a e está no quarto quadrante a
abaixo do eixo (Figura 1.35). Use componentes para encontrar o módulo e a direção de a) ; b) ; c) . Em cada caso faça um diagrama da soma ou da diferença e mostre que os resultados concordam aproximadamente com as respostas numéricas obtidas.
Passo 1
Fala aee, tranquilo??
Vou te propor duas soluções! Começar pela que exige uma sacada.
Belezoca pessoal, no item (b) calculamos , e podemos usar isso a nossa favor agora hehehe
A malandragem nesse passo, é que podemos lembrar que:
Então podemos afirmar que e têm módulos iguais e são opostos em direção.
Ou seja, o módulo do vetor resultante, será:
E
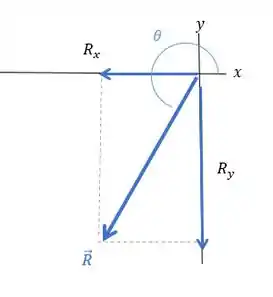
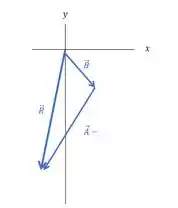
A resultante, , está no terceiro quadrante, com , confirmando nosso cálculo. Onde os vetores e estão dispostos da seguinte maneira:
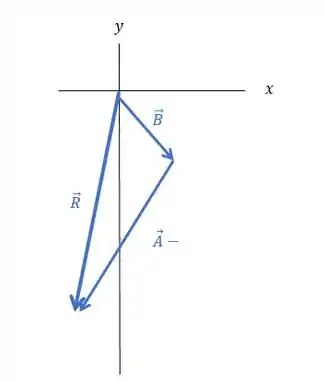
O vetor é o vetor resultante.
Bacana? 😎
Passo 2
A segunda forma é fazendo os cálculos do zero. Então, primeiro, vamos achar os vetores e suas componentes.
Olhando para a figura do problema, podemos decompor os vetores usando seus ângulos. Assim:
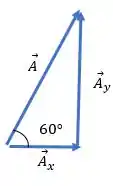
Aqui você pode usar aquela regrinha que diz que a componente que está colada no ângulo ganha um cosseno e a que está separada do ângulo ganha um seno.
Dessa forma, vemos que:
Para o , podemos usar a mesma regra:
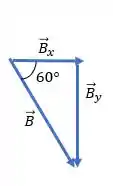
Dessa forma:
Opa, então:
Juntando as componentes de cada eixo:
Tranquilo até aqui? 👀
Passo 3
Opa, e isso bate exatamente com a resposta anterior, como era de se esperar.
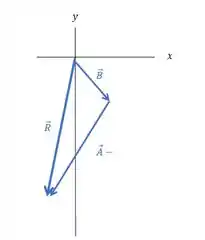
O ângulo também será o mesmo . Beleza?? Pois se tomarmos o ângulo entre e o eixo :
Logo, para pegar o ângulo de até o vetor:
E o módulo será:
É isso!! O que achou? Responde Aí! 😊
Resposta
