Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 3.Problemas Adicionais - Ex. 55

O ponteiro dos minutos de um relógio de parede mede 10   c m da ponta até o eixo de rotação. O módulo e o ângulo do vetor deslocamento da ponta devem ser determinados para três intervalos de tempo. Determine (a) o módulo e (b) o ângulo associado ao deslocamento da ponta entre as posições correspondentes a quinze e trinta minutos depois da hora, (c) o módulo e (d) o ângulo correspondente à meia hora seguinte, e (e) o módulo e (f) o ângulo correspondentes à hora seguinte.

Passo 1

Belezoca galerinha, resolver esse exercício vamos pensar no relógio como estando em um plano cartesiano, com seu centro coincidindo com a origem do plano:

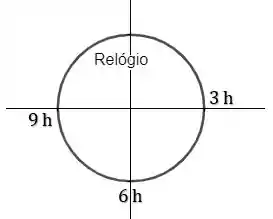
Nesse caso, em que o valor de 3 do relógio represente o semi eixo positivo x e o número 12 represente o semi eixo positivo y , pense em um relógio com um ponteiro para cima e outro 90 ° para a direita. Em vamos calcular qual o valor que representa esse 15 e 30 minutos. 15   m i n u t o s é o próprio valor 3 que atribuímos ao eixo x certo? Agora 30   m i n u t o s em um relógio é marcado no ponto 6 , esse ponto está a 90 ° do anterior, por isso teríamos uma notação em vetores unitário desses ponteiros expressa como:

r = 10   c m i + - 10   c m j

Passo 2

Show de bolinhas, sendo assim, em (a) é solicitado o módulo desse número. A gente calcula esse módulo a partir da equação:

r = 10 2 + - 10 2

r = 200  

r = 14   cm

Passo 3

Agora para o item (b) o enunciado pede o ângulo do deslocamento, esse ângulo é calculado pela através da relação:

tan ⁡ θ = - 10 10 = - 1

Logo o ângulo pode ser encontrado como:

θ = t a n - 1 - 1

θ =   - 45 °

Passo 4

Iradoso, agora passando mais meia hora, no item (c), o ponteiro parte de 6   h para 9   h , olhe para o relógio de parede da casa da sua vó em que você está neste exato momento, primeiro ponteiro em 3   h e segundo ponteiro em 9   h , eles se encontram nesse mesmo eixo imaginário que nós criamos. De forma que eles fiquem totalmente alinhados na horizontal.

O deslocament0 de uma ponta a outra é igual ao módulo total dessa soma, e esse módulo seria a soma dos dois módulos do ponteiro, tal que:

r = 10 + 10

r = 20   cm

Passo 5

Belezera, já no item (d) novamente o ângulo é solicitado entre a ponta e o módulo do ângulo, simplificando, o bizu aqui é que encontrar o ângulo entre o ponteiro 9   h   e   12   h , esse ângulo é igual a 90 ° .

Passo 6

Se for passado mais meia hora (e) nosso movimento no relógio voltará a estaca zero. Teremos então seu deslocamento é 0 .

Passo 7

Tendo um deslocamento nulo, o ângulo em (f) também será nulo.

Resposta

  1. r = 14   c m (b) θ =   - 45 ° (c) r = 20   c m   i (d) θ = 90 ° (e) r = 0 (f) θ = 0 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um manifestante com placa de protesto parte da origem de um sistema de coordenadas x y z , com o plano x y na horizontal. Ele se desloca 40m no sentido negativo do eixo x , faz uma curva de noventa gr
O vetor   A → tem um módulo de 12,0   m e faz um ângulo de 60,0 ° no sentido anti-horário com o semieixo   x positivo de um sistema de coordenadas x y . O vetor B → é dado por 12,0   m i →   +   8,00
Uma partícula sofre três deslocamentos sucessivos em um plano: d 1 →   ,   4,00   m para sudoeste, d 2 →     ,     5,00 para leste, e d 3 →   ,   6,00 em uma direção 60,0 ° ao norte do leste. Use um s
Um barco a vela parte do lado norte-americano do lago Erie para um ponto no lado canadense, 90,0   k m ao norte. O navegante, contudo, termina 50,0   k m a leste do ponto de partida. (a) Que distância
O oásis B está 25K m a leste do oásis A . Partindo do oásis A , um camelo percorre 24K m em uma direção 15 ° ao sul do leste e 8K m para o norte. A que distância o camelo está do oásis B ?