Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.Problemas Adicionais - Ex. 70

Um vetor d → tem um módulo de 3,0   m e aponta para o sul. Determine (a) o módulo e (b) a orientação do vetor 5,0 d → . Determine (c) o módulo e (d) a orientação do vetor - 2,0 d → .

Passo 1

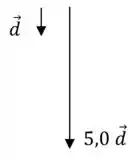
(a) Se o vetor d → tem módulo 3,0   m , quando multiplicarmos ele por 5,0 , o seu módulo aumentará exatamente nessa proporção:

d → = 3,0   m

  5,0   d → = 15,0   m

Passo 2

(b) A orientação do vetor continua sendo para o sul, já que a multiplicação por um escalar diferente de zero nunca muda a direção de um vetor, e só muda o seu sentido se o escalar for negativo.

Passo 3

(c) A mesma lógica de antes continua valendo para o cálculo do módulo:

d → = 3,0   m

- 2,0   d → = 6,0   m

Passo 4

(d) Dessa vez, a direção do vetor continuará sendo preservada, mas o fato de que - 2,0 < 0 vai alterar o sentido do vetor d → :

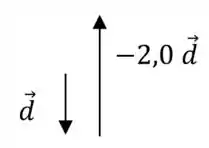
Ou seja, o novo vetor aponta para o norte.

Resposta

(a) O módulo será 15   m .

(b) O vetor apontará para o sul.

(c) O módulo será 6,0   m .

(d) O vetor apontará para o norte.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine A → ∙ B → para os seguintes vetores: (a) A → = 3 i ^ - 6 j ^ ,B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;
Determine os ângulos entre os vetores A → e B → dados: (a) A → = 3 i ^ - 6 j ^ , B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;
Determine A → ∙ B → para os seguintes vetores: (a) A → = 3 i ^ - 6 j ^ ,B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;
Uma partícula de 2,0 kg sofre um deslocamento de Δ r → = 3,0m i ^ + 3,0m j ^ + - 2 , 0m k ^ . Durante esse deslocamento, uma força constante F → = 2 , 0N i ^ - 1 , 0N j ^ + 1 , 0N k ^ atua sobre a par
Determine os ângulos entre os vetores A → e B → dados: (a) A → = 3 i ^ - 6 j ^ , B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;