Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.7 - Ex. 32

Para os vetores A   → e B → incicados na Fígura 1.34 use diagramas em escala para determinar a) a soma vetorial   A → + B → b) a diferença vetorial A → – B → . Use suas respostas para encontrar o módulo e a direção de c) – A → – B → e d) B → – A → . (Veja também o Exercício 1.29 para usar um método alternativo na solução deste problema.)

Passo 1

E aí! tudo certinho?

Nesse problema foi dado dois vetores e nosso objetivo é calcular algumas operações de soma e subtração entre esses vetores.

Parece complicado? 🤔

Antes de somar vetores, devemos entender que precisamos inicialmente deixa-los com mesmo sentido. Para que isso seja possível, devemos lembrar conceitos fundamentais de decomposição de vetores.

Veja só! 😉

Passo 2

  1. Para somar A → + B → , devemos decompor o vetor B → nas direções x e y. A já pode ser definido como A → = (-8.0m) y → .

    2. Para rescrever B → vamos escreve-los em função de senos e cossenos da seguinte forma:

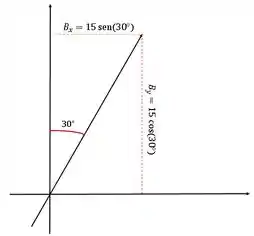
    Então temos que B x   =   15   s e n ( 30 ° )   =   7,5 m e B y   =   15   c o s ( 30 ° )   ≈   13,0 m . Desta forma podemos somar nossos vetores.

    ( A x   +   B x )   =   ( 0 m )   +   ( 7,5 ) m   =   7,5 m

    e

    ( A y   +   B y )   =   ( - 8,0 m )   +   ( 13,0 m )   =   5,0 m

    Então temos que A → + B → = 7,5 i + 5,0 j m   .

    Tranquilo até aqui? 😉

    Passo 3

  2. Agora queremos fazer A → - B → . Entretanto já temos os valores decomposto em x e y dos nosso vetores.

    3. ( A x   -   B x )   =   ( 0 m )   –   ( 7,5 m )   =   - 7,5 m

    e

    ( A y   +   B y )   =   ( - 8,0 m )   –   ( 13,0 m )   =   - 21,0 m

    Desta forma podemos escrever que A →   - B → =   - 7 , 5 i + 21 , 0 j m .

    Bacana, não é? 😁

    Passo 4

  3. Agora temos que calcular – A → - B → . Podemos escrever que

    4. - A → - B →   =   - ( A → + B → )   =   - ( 7 , 5 i + 5.0 j ) m  

    Está acompanhando? 👀

    Passo 5

  4. E para B →   -   A →

B →   –   A →   =   - A →   –   B → =   -   - 7.5 m   21.0 m =   7,5 i + 21,0 j m

E aí! o que achou? Responde Aí! 😉

Resposta

  1. A → + B → = 7,5 i + 5,0 j m
  2. A →   - B → =   - 7 , 5 i + 21 , 0 j m
  3. - A → - B →   =   - A → + B → = - 7,5 i + 5,0 j m
  4. B →   –   A →   =   - ( A →   –   B → )   = 7,5 i + 21,0 j m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por que a seguinte situação é impossível? Uma skatista desliza ao longo de um trajeto circular. Ela define certo ponto no círculo como sua origem. Mais tarde, passa por um ponto no qual a distância qu
Um avião voa do campo-base para o Lago A, a 280k m de distância na direção 20,0 ° nordeste. Após soltar os suprimentos, ele voa para o Lago B, que fica a 190 km em 30,0 ° a noroeste do Lago A. Determi
Um carrinho de montanha-russa move-se a 200p é s é horizontalmente e sobe 135p é s é em um ângulo de 30,0 ° acima da horizontal. Depois, viaja 135p é s é em um ângulo de 40,0 ° para baixo. Qual é seu
Os vetores deslocamento A → e B → mostrados na Figura P1.34 têm módulos de 3,00m . A direção do vetor A: é θ=30,0 ° . Encontre graficamente a) A → + B → b) A → - B → c) B→ - A → d) A → - 2 B → (Inform
Considere os três vetores de deslocamento A →=( 3i ^–3j ^ )m , B →=(i ^–4j ^ )m e C →=( 2i ^+5j ^ )m . Use o método das componentes para determinar a) o módulo e a direção do vetor D →=A →+ B →+ C → b