Um homem está parado no alto de um edifício de de altura e atira uma pedra com velocidade de módulo de formando um ângulo inicial de acima da horizontal.
Despreze a resistência do ar. Calcule a) a altura máxima acima do telhado atingida pela pedra; b) o módulo da velocidade da pedra imediatamente antes de ela atingir o solo; c) a distância horizontal entre a base do edifício e o ponto onde ela atinge o solo. d) Faça diagramas para o movimento.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular (a) a alturam máxima atingida pela pedra, (b) o módulo da sua velocidade imediatamente antes de ela atingir o solo, (c) a distância horizontal alcançada e (d) esboçar os diagramas diagramas para o movimento.
Vamos tomar como origem as coordenadas no telhado, e consideraremos como para cima.
Depois de atirada, a pedra se move com movimento de projetil. Então, a aceleração em cada eixo vai ser dada por:
Então, vamos esboçar a situação e separar as componentes da velocidade em e em :
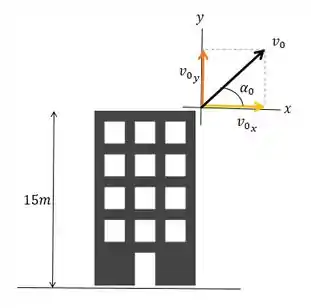
Assim, vamos ter:
E
Com isso em mãos, vamos usar as equações do movimento uniforme (na horizontal) e do movimento uniformemente variado (na vertical) para determinar o que se pede.
Vamos lá!
Passo 2
a) Na altura máxima, a velocidade na verticial é igual a zero: .
E, temos que:
Como não precisamos do tempo, , podemos utilizar a equação de Torricelli:
Assim, isolando temos a distância horizontal:
E substituindo os dados:
Passo 3
Nós vamos encontrar a velocidade resolvendo seus componentes e :
Como a aceleração em : .
Para encontrarmos a velocidade em vamos utilizar novamente a equação deTorricelli:
Agora temos que (negativo porque no chão a pedra está abaixo da sua posição inicial) e .
é negativo porque no chão a rocha está descendo. Assim, temos:
Passo 4
b) E então podemos calcular o módulo da velocidade:
Substituindo os valores das componentes, temos:
Passo 5
c) Vamos utilizar o movimento vertical (componente ) para encontrar o tempo, , em que a rocha está no ar.
Temos que:
Passo 6
c) Então, vamos usar esse tempo, para calcular a distância alcançada, , na horizontal:
Vamos utilizar a equação:
Assim, substituindo os dados, temos:
Passo 7
d) E os gáficos ficam da seguinte maneira:
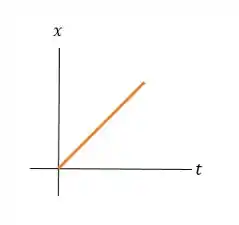
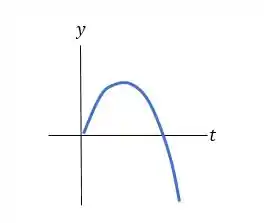
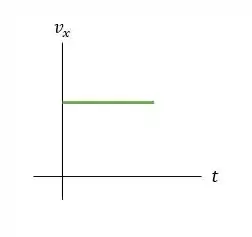
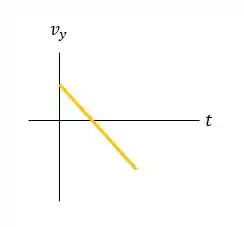
Valeu, galera! Até a próxima! 😉