Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Perguntas Objetivas - Ex. 08
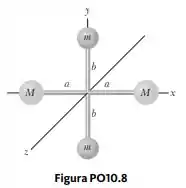
A Figura PO mostra um sistema de quatro partículas unidas por barras leves e rígidas. Suponha que e seja maior que . Ao redor de quais eixos coordenados o sistema tem o menor e o maior momento de inércia? o eixo o eixo o eixo . O momento de inércia tem o mesmo pequeno valor para os dois eixos. O momento de inércia é o mesmo para todos os três eixos.
Passo 1
Vem comigo que a gente resolve essa juntos!
O momento angular de uma partícula é dado por:
Onde é massa da partícula e é distância da partícula até o eixo de rotação.
O momento de inércia total do sistema é dado pela soma dos momentos de inércia de cada partícula.
Passo 2
O maior momento de inercia vai acontecer quando consideramos um eixo onde o momento de inércia de todas as partículas é levado em conta.
Isso ocorre para o eixo de rotação pois teremos a contribuição das partículas.
Então nossa letra é a .
Passo 3
Para ver em qual eixo ocorre o menor momento de inércia temos que escolher um eixo que passe pelo maior número de partículas, pois aí o momento de inércia delas vai ser zero, já que .
Temos duas opções, ou o eixo ou o . Sabemos que , então que vai determinar o momento de inércia vai ser a massa das partículas.
Como a melhor escolha de eixo vai ser o , pois as partículas de massa não vão contribuir para o momento de inércia.
Com isso a letra certa é a .