Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.Problemas Adicionais - Ex. 78
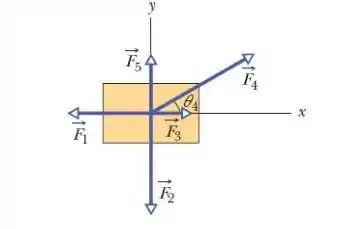
Na vista superior da , cinco forças puxam uma caixa de massa . Os módulos das forças são , , , e; o ânguloé . Determine a aceleração da caixa (a) na notação dos vetores unitários e como (b) um módulo e (c) um ângulo em relação ao semieixo positivo.
Passo 1
Belezoca de motoca galerinha, no nossos sistema temos forças em sentidos diferentes atuando sobre o bloco:
Em especifico, faz um ângulo com o semieixo positivo . Dessa forma, a força resultante será a soma vetorial de todas as forças que atuam:
E pra facilitar nossas contas, podemos fazer a soma separadamente em cada eixo, decomponto as forças e somando nos eixos respectivos:
Então é hora de decompor, vamos decompor o nos eixos x e y.
A partir disso podemos juntar as forças em x e as forças em y.
Passo 2
Para encontrar a aceleração em vetores unitários pedida em (a) devemos mexer com a equação , isolando a aceleração e obtendo que:
A partir disso, para a força em cada eixo conseguimos obter a aceleração em vetores unitários, saca só:
Passo 3
O módulo em (b) fica super fácil de ser calculado agora que sabemos a aceleração em vetores unitários, apenas utilizamos o Teorema do Tio piti () e chegamos no resultado.
Passo 4
Para a angulação de (c) usaremos a inversa da tangente, pois temos os dois catetos de um triângulo retângulo que são os vetores unitários da aceleração, chegando nesse resultado: