Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 74
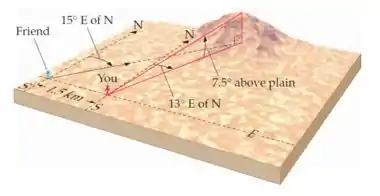
Você e um amigo estão caminhando por uma região grande e plana e decidem determinar a altura de um distante pico de montanha, e também a distância horizontal entre vocês e o pico (Figura 1-19). Para isto, você se coloca em um ponto e verifica que sua linha de visada até o topo do pico é inclinada de em relação à horizontal. Você também anota a orientação do pico com relação àquele ponto: a leste do norte. Você se mantém na posição original e seu amigo caminha 1,5km para o oeste. Então, ele divisa o pico e verifica que sua linha de visiada tem uma orientação de a leste do norte. Qual a distância da montanha à sua posição e qual a altura do pico em relação à de sua posição?
Passo 1
Fala! Então, aqui você e seu amigo, por alguma razão, querem a distância entre você e o pico e também a altura do pico da montanha.
Ele nos dá algumas informações geométricas para a gente chegar lá. Então o que vamos fazer é desenhar as situações que temos e ir montando equações como que a gente tira desses desenhos até chegar no resultado. Vamos na fé mesmo!
Vamos começar por desenhar a situação vista de cima pras coisas ficarem mais claras, ok?
Você e seu amigo estão separados por . A visada (linha entre o observador e o ponto observado, no caso, o pico da montanha) do seu amigo faz com a direção norte e a sua faz com a direção norte. O desenho fica:
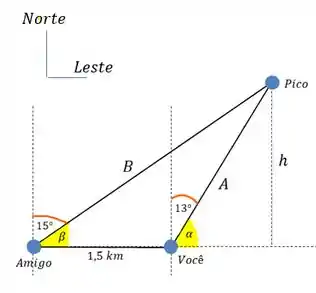
é uma distância auxiliar que a gente colocou, para que apareçam triângulos retângulos na figura, e também são ângulos auxiliares. Primeiro queremos encontrar a distância que separa você da montanha. E depois a altura da montanha, tá? Bora lá!
Passo 2
Olha comigo esses 2 triângulos retângulos que podemos destacar na figura:
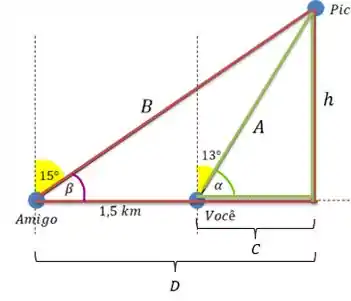
Pelo triângulo em vinho, temos que:
Pelo triângulo verde temos:
Podemos igualar as duas expressões para :
E então:
Passo 3
Vamos continuar analisando os nossos 2 triângulos retângulos.
Para o triângulo vinho:
E para o triângulo verde:
Note pela figura também que:
Substituindo as expressões de D e C que encontramos, temos:
Mas lembra que no passo 2 encontramos:
E substituindo essa expressão que encontramos para na nossa desse passo mesmo:
Lembra que seno sobr cosseno é tangente, então se a gente tem o inverso disso, temos o 1 sobre tangente:
Passo 4
Agora podemos olhar a figura e ver que:
E então podemos substituir esses valores de e na equação anterior e encontramos :
Passo 5
E agora falta encontrar a altura do pico, , acima da nossa posição. O enunciado diz que a nossa linha de visão até o pico forma um ângulo de com o plano horizontal.
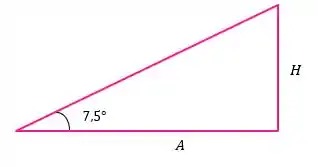
Olhando para esse triângulo retângulo temos:
Já que sabemos que a distância entre nós e a montanha é , podemos calcular essa altitude fazendo:
Resposta
A distância até a montanha é , e a altitude é .