Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 106

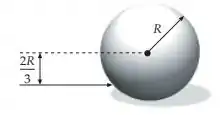
Uma bola de bilhar, inicialmente em repouso, recebe uma forte tacada. A força é horizontal e aplicada a uma distância 2 R 3 abaixo da linha diametral, como mostra a figura. A rapidez da bola imediatamente após a tacada é v 0 e o coeficiente de atrito cinética entre a bola e a mesa é μ c . (a) Qual é a rapidez angular da bola imediatamente após a tacada? (b) Qual é a rapidez da bola assim que ela começa a rolar sem deslizar? (c) Qual é a energia cinética da bola imediatamente após a tacada?

Passo 1

Bora pra mais uma! Acompanha aqui comigo: com a tacada embaixo do diâmetro da bola, ela vai girar no sentido anti-horário, certo? Então, o ponto de contato da bola com o chão vai se mover para a direita. Daí, vai surgir a força de atrito, oposta ao movimento, e então ela vai apontar para a esquerda. Sacou?

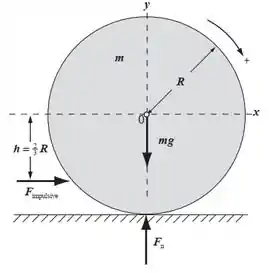
No momento da tacada, a situação vai ter essa cara aqui:

Depois, o movimento de translação da bola vai ter essa outra cara aqui:

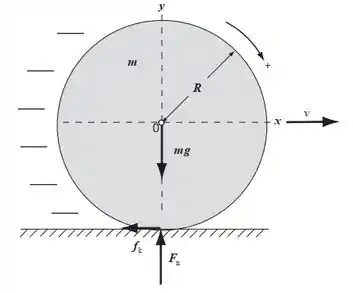
Passo 2

  1. Aplicando a segunda lei de Newton para a rotação (primeira figura):

    2. ∑ τ = I c m α

    F m h = - I c m ω 0 Δ t

    ω 0 = - F m h Δ t I c m

    Como nós sabemos lá do capitulo de quantidade de movimento:

    F m Δ t = m v 0

    Substituindo isso ali em cima:

    ω 0 = m v 0 h 2 5 m R 2

    ω 0 = 5 v 0 h 2 R 2

    Do enunciado, h = 2 R / 3 .

    ω 0 = - 5 v 0 2 R 3 2 R 2 = - 5 v 0 3 R

    Passo 3

  2. Agora vamos aplicar a segunda lei de Newton para a segunda situação:

    3. F y = 0 → N = m g → F a t = μ c m g

    F x = - F a t = m a → - μ c m g = m a → a = - μ c g

    ∑ τ = I α

    F a t R = 2 5 m R 2 α

    α = 5 μ c g 2 R

    Do movimento da bola a gente sabe que:

    ω = ω 0 + α t = ω 0 + 5 μ k g t 2 R

    v = v 0 + a t = v 0 - μ c g t

    Se liga: sempre que falar que o corpo rola sem deslizar, a gente pode usar que v = ω R .

    v 0 - μ c g t = ω 0 + 5 μ k g t 2 R R

    v 0 - ω 0 R = 5 μ c g t 2 + μ c g t

    Da letra (a) conseguimos escrever a velocidade angular em função da velocidade escalar.

    t = v 0 - ω 0 R 7 2 μ c g = v 0 - - 5 v 0 3 R R 7 2 μ c g

    Simplificando, vamos obter:

    t = 16 v 0 21 μ c g

    Substituindo na velocidade, vamos encontrar:

    v = v 0 - μ c g 16 v 0 21 μ c g

    v = 5 v 0 21

    Passo 4

  3. A energia cinética inicial é dividida entre rotacional e translacional por:

K i = K t + K r = m v 0 2 2 + I ω 0 2 2

Conhecemos o momento de inércia da esfera!

K i = m v 0 2 2 + 1 2 2 5 m R 2 - 5 v 0 3 R 2

K i = m v 0 2 2 + 5 m v 0 2 9

K i = 19 m v 0 2 18

Resposta

  1. ω 0 = - 5 v 0 3 R
  2. v = 5 v 0 21
  3. K i = 19 m v 0 2 18
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma argola de massa M e raio R , que eola sem deslizar, o que é maior, sua energia cinética translacional ou sua enérgica cinética em relação ao centro de massa? (a) A energia cinética translacio
Uma casca cilíndrica fina e um cilindro maciço e uniforme rolam horizontalmente, sem deslizar. A rapidez da casca cilíndrica é v . O cilindro maciço e a casca cilíndrica encontram uma rampa que sobem,
Um cilindro homogêneo de 60 k g tem um raio de 18 c m e está rolando sem deslizar, sobre um piso horizontal, com uma rapidez de 15 m / s . Qual foi a mínima quantidade de trabalho necessária para lhe
Uma casca esférica fina rola descendo um plano inclinado, sem deslizar. Se a aceleração linear do centro de massa da casca é 0,20 g , qual é o ângulo de inclinação do plano com a horizontal?
Um corpo está rolando sem deslizar. Qual é a porcentagem da energia cinética total que tem a forma de energia cinética de translação, se o objeto é (a) uma esfera uniforme, (b) um cilindro uniforme ou