Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 71
Você é um astronauta fazendo experimentos de física na lua. Você está interessado na relação experimental entre a distância de queda, , e o tempo decorrido, , de objetos que caem a partir do repouso. Você coletou alguns dados de uma moeda caindo, que estão representados na tabela abaixo:
Você espera que uma relação geral entre a distância e o tempo seja , onde e são constantes a serem determinadas experimentalmente. Para fazer isso, crie um gráfico log-log dos seguintes dados: (a) faça o gráfico de vs. , com como variável da ordenada e como variável da abcissa. (b) Mostre que se você tomar o logaritmo de cada lado da sua relação esperada, você encontrará . (c) Comparando essa relação linear com o gráfico dos dados, estime os valores de e . (d) Se você deixar cair uma moeda, quanto tempo ela deveria levar para cair ? (e) No próximo capítulo, nós vamos mostrar que a relação esperada entre e é , onde é a aceleração do objeto. Qual é a aceleração de objetos em queda na lua?
Passo 1
(a) Para fazer o gráfico pedido podemos colocar os dados do enunciado em um programa de planilhas para gerar o gráfico de em função de . Assim teremos um gráfico desse tipo:
Na verdade o que o programa faz é calcular o log de todos os dados que o enunciado nos deu, e depois montar um gráfico. Aí você coloca os resultados de como seu eixo horizontal, e o de como seu eixo vertical.
Nós usamos um programa, mas você também pode fazer isso usando uma calculadora científica, o que daria muuuuito mais de trabalho, mas ficaria igualzinho, ok.
Como é a variável da ordenada, podemos nomea-la de . E nomear de .
Fazendo num programa de planinhas, o computador nos dá uma equação para essa reta:
Vamos substituir nossos novos nomes das variáveis nessa equação
Percebe que agora sim, isso tem cara de reta. Vamos seguir!
Obs: é bom desenhar esse gráfico no computador mesmo, e achar essa equação da reta que ele vai te dar, tá bem? Para suas continhas baterem com o gabarito.
Passo 2
(b) Agora vamos aplicar o logaritmo na equação geral que foi dada no enunciado:
Aplicamos os log dos dois lados
Para reescrever essa equação, a gente precisa lembrar das propriedades de log. Vamos lembrar da propriedade da soma/produto. Quando a gente tinha no argumento do log um produto de dois valores, a gente podia reescrever isso como a soma do log desses valores.
Por exemplo:
Aplicando isso na nossa situação, temos o produto entre e , então vamos fazer
Agora a gente pode lembrar da propriedade do peteleco. Se a gente tinha um expoente dentro do argumento do log, ele podia sair multiplicando pelo log, por exemplo
Aí no nosso caso
Se torna:
Passo 3
c) Se a gente usar a nomemclatura do passo 1,
Podemos escrever a relação que encontramos no item b, como:
Essa é a equação da reta que a gente esboçou no passo 1. Vamos tentar encontrar os valores de e comparando essa equação com a equação que tiramos do gráfico:
O ponto onde o gráfico cruza o eixo é , e isso vai ser igual a :
E para encontrar só precisamos olhar para o coeficiente angular da reta:
Passo 4
(d) Então nossa equação é:
Para descobrir o tempo que a moeda demora a cair , vamos substituir na nossa equação
Passo 5
(e) Se a equação é do tipo , então podemos comparar com a nossa equação para encontrar o valor de :
Vamos igualar as duas expressões para :
Resposta
(a)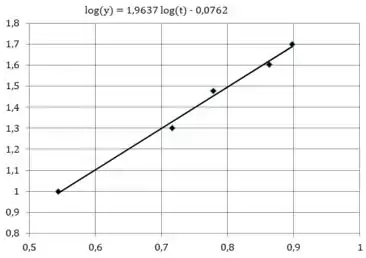 
(b) .
(c) e .
(d) .
(e) .