Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 22
Você deseja localizar o centro de gravidade de um objeto achatado e de formato arbitrário. Você pendura o objeto de um ponto e um fio de prumo do mesmo ponto. Então, você traça uma linha vertical no objeto, representando o fio de prumo. Depois, você repete o procedimento, usando um outro ponto de suspensão. O centro de gravidade será a interseção das linhas traçadas. Explique o(s) princípio(s) que existe(m) por trás disto.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro, o fio de prumo é um fio com um pesinho na ponta. Por causa desse pesinho, esse fio fica sempre certinho na direção vertical, onde a atua a força gravitacional. Então ele representa a direção da força gravitacional (força peso) sobre o objeto.
Aí o enunciado diz que a gente pode pegar um objeto achatado em formato qualquer. Só para ilustrar, imagina que você tem na sua casa aí um quadrado achatado muito fofo em formato de nuvem:
Percebe que o formato dela é bem irregular, né? Não tem nenhuma simetria nem nada. Então, o objeto pode ser assim.
Aí a gente consegue achar o centro de massa desse objeto pendurando ele em um ponto e pendurando um fio de prumo no mesmo ponto, traçando uma linha onde esse fio de prumo passa. E repetindo o procedimento em outro ponto. Aí o CM é a interseção dessas linhas:
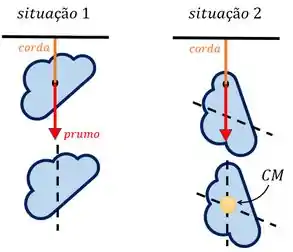
Aí ele quer saber o principio físico por trás desse experimento aí. Vamos refletir!
Passo 2
Cara, a situação é que quando você pendura o objeto e espera até que ele fique paradinho, você estará encontrando posições nas quais a gravidade não exerce torque no objeto. E por isso mesmo ele fica parado, sem girar.
E qual é o indicativo que uma força não gera torque num objeto? É quando a linha de ação da força passa pelo centro de massa do objeto. Então, na nossa situação, a força gravitacional (peso) está passando pelo centro de massa do objeto quando ele para de girar.
E como o prumo mostra para gente a direção onde a força gravitacional está atuando, a gente consegue marcar no objeto a linha de ação da força gravitacional, que está passando pelo centro de massa.
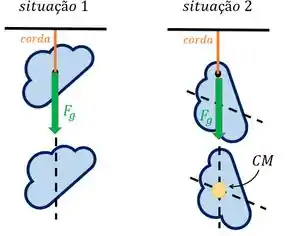
Como a gente faz isso duas vezes, temos duas linhas no nosso objeto que passam pelo centro de massa dele. Se as duas passam pelo centro de massa e elas só se interceptam uma vez, o ponto de inteseção é o centro de massa!
É por isso que esse experimento funciona. Se você pendurar o objeto em um terceiro ponto, a linha traçada vai passar também pelo CM.
Resposta
Discussão nos passos