Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas adicionais - Ex. 112
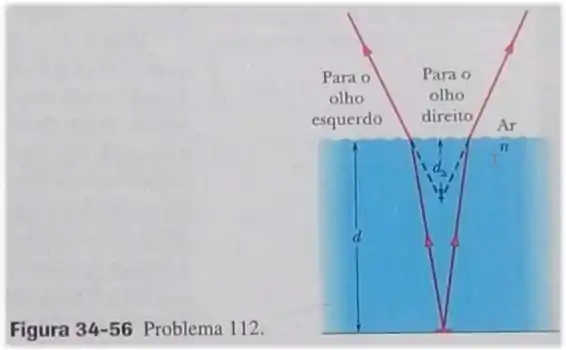
Você olha para baixo, em direção a uma moeda que está no fundo de uma piscina de profundidade e índice de refração (Fig.34-56). Como você observa a moeda com dois olhos, que interceptam raios luminosos diferentes provenientes da moeda, tem a impressão de que a moeda se encontra no lugar onde os prolongamentos dos raios interceptados se cruzam, a uma profundidade . Supondo que os raios da Fig. 34-56 não se desviam muito da vertical, mostre que . (Sugestão: use a aproximação, válida para ângulos pequenos, de que .
Passo 1
Vamos definir alguns pontos para ajudar a nos encontrar em nossa imagem. Seja o ponto que o raio sai da água em direção ao olho esquerdo e seja o ponto que o raio sai da água em direção ao olho direito. O ponto na superfície da água e que é equidistante de e é chamado de . A moeda se encontra no ponto que é o ponto mais fundo a uma distância da superfície. Outro ponto importante é que está a uma distância e também é equidistante de e .
Passo 2
Agora que temos todos nossos pontos definidos, vamos começar. Seja e
e
Passo 3
Lembrando da nossa lei de refração
e que para pequenos ângulos
Temos que
Assim teremos que
Resposta
Vide o passo a passo.