Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 44

Considere dois corpos com m 1   >   m 2 conectados por uma corda leve que passa sobre uma polia tendo um momento de inércia de I em torno de seu eixo de rotação conforme mostrado na Figura P10.44. A corda não escorrega na polia nem estica. A polia gira sem atrito. Os dois corpos são liberados do repouso separados por uma distância vertical de 2 h .

  1. Use o princípio de conservação de energia para encontrar as velocidades translacionais dos corpos à medida que passam um pelo outro.
  2. Encontre a velocidade angular da polia nesse momento.

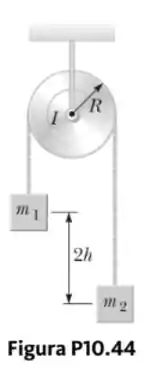
Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Pegue os dois objetos, polia e Terra como o sistema. Se negligenciarmos a fricção no sistema, então a energia mecânica é conservada e podemos afirmar que o aumento da energia cinética do sistema é igual à diminuição da energia potencial. Uma vez que K i = 0 (o sistema está inicialmente em repouso), nós temos:

Δ K = K f - K i = 1 2 m 1 v 2 + 1 2 m 2 v 2 + 1 2 I ω 2

Onde m 1   e  m 2 têm uma velocidade comum. Mas v = R ω de modo que:

Δ K = 1 2 m 1 + m 2 + I R 2 v 2

Passo 2

Vemos que o sistema perde energia potencial devido ao movimento de m 1 , e ganha energia potencial por causa do movimento de m 1 . A Aplicação da lei da conservação de energia, Δ K + Δ U = 0 nos dá:

1 2 m 1 + m 2 + I R 2 v 2 + m 2 g h - m 1 g h = 0

v = 2 m 1 - m 2 g h m 1 + m 2 + I R 2

Como v = R ω , então:

ω = v R = 2 m 1 - m 2 g h m 1 R 2 + m 2 R 2 + I

Resposta

v = 2 m 1 - m 2 g h m 1 + m 2 + I R 2   e   ω = v R = 2 m 1 - m 2 g h m 1 R 2 + m 2 R 2 + I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ciclista acelera uniformemente a partir do repouso. Após 8,0s , as rodas completam 3,0v o l t a s . (a) Qual é a aceleração angular das rodas? (b) Qual é a rapidez angular das rodas ao final dos 8,
A fita em um videocassete VHS padrão tem um comprimento total de 246 m , o suficiente para operar durante 2,0 h . Quando no início, o carretel cheio tem um raio externo de 45 m m e um raio interno de
Uma roda varre 5,0r a d em 2,8s ao ser levada ao repouso com aceleração angular constante. Determine a rapidez angular inicial da roda ao começar a ser freada.
Uma bicicleta tem rodas de 0,750 m de diâmetro. O ciclista acelera a partir do repouso, com aceleração constante, até 24,0k m / h , em 14,0 s . Qual é a aceleração angular das rodas?
Marte orbita em torno do Sol com um raio orbital médio de 228 G m ( 1 G m = 10 9 m ) e tem um período orbital de 687 dias. A Terra orbita em torno do Sol com um raio orbital médio de 149,6 G m . (a) A