A função energia potencial para um sistema de partículas é determinada por U ( x )=– x 3 + 2 x2 +3 x , em que x é a posição de uma partícula no sistema.a.Determine a força F x sobre a partícula como uma função de x .b.Para quais valores de x a força é igual a zero?c.Trace U ( x ) por x e F x por x e indique pontos de equilíbrio estável e instável.

a. ∴ F x = - U ' x = 3 x 2 - 4 x - 3 b. x 1 ≅ 1,87 e x 2 ≅ - 0,54 c.Vide Passo 3.

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 66

A função energia potencial para um sistema de partículas é determinada por , em que é a posição de uma partícula no sistema.

a.Determine a força sobre a partícula como uma função de .

b.Para quais valores de a força é igual a zero?

c.Trace por e por e indique pontos de equilíbrio estável e instável.

Passo 1

a.Amores, do teorema Força x Energia Potencial, a gente tem essa relaçãozinha aqui:

Onde representa a energia potencial e a posição da(s) partícula(s) envolvida(s), blz?

Nisso, basta a gente derivar a funçãozinha pra encontrar uma expressão pra força em função de , tudo bem?

A gente vai ter:

Passo 2

b.Pra saber esses valores, basta a gente igualar a expressão pra a zero, resolvendo uma equaçãozinha de segundo grau básica, fechou?

Com isso, a gente vai ter:

Agora é só jogar em bhaskara e a gente resolve, assim:

Essas vão ser as posições das partículas pra força nula. Sendo a força dada em newtons, essas posições são dadas em metros, tudo bem?

Passo 3

c.Temos pra e respectivamente:

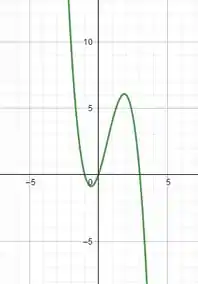
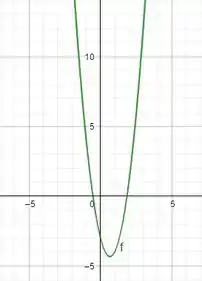
Os pontos de equilíbrio a gente observa pelo gráfico de . Eles vão ser sempre os pontos de máximo e de mínimo que a função apresentar.

Como faz pra, a partir da função, determinar esses pontos mesmo?

Bom, isso a gente acabou de fazer no Passo 2, que foi por derivar a função original e determinar os pontos em que a derivada se anulava. Assim, os pontos de equilíbrio são justamente:

Tá, mas qual é o estável e qual o instável?

A regrinha é que os pontos de mínimo, por serem “poços” de energia potencial, são pontos de equilíbrio estável, uma vez que qualquer perturbação feita na partícula vai fazer ela retornar à posição de mínimo de energia potencial.

Já os pontos de equilíbrio instáveis são pontos de máximo. A partícula na posição de máximo, por mais que estando estável, sofrendo qualquer perturbação, vai rapidamente mudar de posição, pra uma mais estável ainda.

Com isso, a gente verifica que é ponto de equilíbrio estável e é ponto de equilíbrio instável, certinho?

Resposta

b. e

c.Vide Passo 3.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Durante o semestre de primavera do MIT, os estudantes de dois dormitórios vizinhos travam batalhas com grandes catapultas feitas com meias elásticas montadas na moldura das janelas. Um balão de aniver

A Fig. 7-36 mostra a força elástica Fx em função da posição x para o sistema massa mola da Fig. 7-9. A escala vertical do gráfico é definida por F x=160,0N . Puxamos o bloco até x=12c m e o liberamos.

O bloco na Fig. 7-9a está sobre uma superfície horizontal sem atrito e a constante elástica é 50N / m . Inicialmente, a mola está relaxada e o bloco está parado no ponto x= 0 . Uma força com módulo co

A Fig. 8-47 mostra um gráfico da energia potencial U em função da posição x para urna partícula de 0,200k g que pode se deslocar apenas ao longo de um eixo x sob a influência de uma força conservativa

A energia potencial de uma molécula diatômica (um sistema de dois átomos, como H2 ou O2) é dada por U = A r 12 - B r 6 onde r é a distância entre os átomos da molécula e A e B são constantes positivas