Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 65

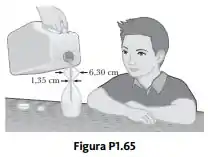
Uma criança adora olhar enquanto você enche uma garrafa de plástico transparente com xampu (Fig. P1.65). Cada corte horizontal da garrafa é circular, mas os diâmetros dos círculos têm valores diferentes. Você derrama o xampu colorido brilhante na garrafa a uma taxa constante de   16,5   c m 3 / s . A que taxa cresce seu nível na garrafa

a) em um ponto onde o diâmetro da garrafa é 6,30   c m ?

b) em um ponto onde o diâmetro é 1,35   c m ?

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer mais uma questãozinha aqui?

Vem comigo!

Observe na figura que o raio da seção transversal horizontal da garrafa é um máximo ou mínimo relativo nos dois raios citados no problema; assim, reconhecemos que conforme o nível do líquido sobe, a taxa de tempo da mudança do diâmetro da seção transversal será zero nestas posições.

O volume de uma seção transversal fina específica do shampoo de espessura h e área A é V = A h , onde A = π r 2 = π D 2 4 . Diferenciando o volume em relação ao tempo:

d V d t = A d h d t + h d A d t = A d h d t + h d d t π r 2 = A d h d t + 2 π h r d r d t

Como os raios dados são um valor máximo e mínimo d r d t = 0 , então:

d V d t + A d h d t = A v → v = 1 A d V d t = 1 π D 2 4 d V d t = 4 π D 2 d V d t

onde v = d h d t é a velocidade com que o nível do fluido sobe.

Passo 2

Letra a:

Para D = 6.30 c m :

v = 4 π ( 6.30 c m ) 2 16.5 c m 3 s = 0.529 c m s

Passo 3

Letra b:

Para D = 1.35 c m :

v = 4 π ( 1.35 c m ) 2 16.5 c m 3 s = 11.5 c m s

Resposta

  1. 0.529 c m s
  2. 11.5 c m s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calculando o volume do pulmão em humanos. Em humanos, oxigênio e dióxido de carbono são trocados no sangue dentro de bolsas chamadas alvéolos nos pulmões. Os alvéolos oferecem uma grande superfície pa
Os indivíduos variam bastante no volume total dos pulmões. A Figura P1.94 mostra os resultados da medição do volume total dos pulmões e volume alveolar médio de seis indivíduos. Por esses dados, o que
Você é o líder de equipe em uma empresa farmacêutica. Vários técnicos estão preparando amostras, e você deseja comparar as densidades delas (densidade = massa/volume) usando os valores de massa e volu
Se considerarmos que os alvéolos são esféricos, qual é o diâmetro de um alvéolo típico? (a) 0,20 mm; (b) 2 mm; (c) 20 mm; (d) 200 mm.
Estima-se que a densidade média de matéria no universo corresponde a da ordem de 0,2 átomos de hidrogênio por m 3 . (a) Estime a massa total contida dentro do raio do universo; (b) Estime o número tot