Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 53
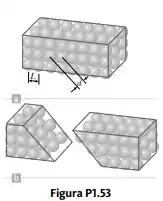
Um sólido cristalino consiste em átomos empilhados em uma estrutura de treliça repetitiva. Considere um cristal conforme mostrado na Figura P1.53a. Os átomos residem nos cantos de cubos de lado . Uma evidência para o arranjo regular de átomos vem das superfícies planas ao longo das quais um cristal é separado, ou clivado, quando se quebra. Suponha que um cristal se parta ao longo de uma face diagonal conforme mostrado na Figura P1.53b. Calcule o espaço entre dois planos atômicos adjacentes que se separam quando o cristal se parte.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Na figura, podemos ver que o espaçamento entre os planos diagonais é a metade da distância entre átomos diagonalmente adjacentes em um plano reto. Esta distância diagonal pode ser obtida do através do teorema de Pitágoras:
Assim, uma vez que os átomos são separados por uma distância , os planos diagonais são separados por: