Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 68
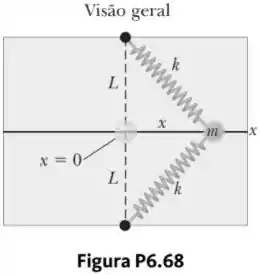
. Uma partícula de massa é presa entre duas molas idênticas sobre um tampo de mesa horizontal, sem atrito. Ambas as molas têm constante elástica e estão inicialmente não distendidas e a partícula está em . A partícula é puxada a uma distância ao longo de uma direção perpendicular à configuração inicial das molas, como mostrado na Figura P. Mostre que a força exercida pelas molas sobre a partícula é
Mostre que a energia potencial do sistema é
Trace um gráfico de por e identifique todos os pontos de equilíbrio. Considere e . Se a partícula for puxada para a direita e depois solta, qual será sua velocidade escalar quando ela atingir ?
Passo 1
Vamos juntos resolver esse problema!
Vamos analisar cada item separadamente para a gente não se embolar. Vamos começar com o item .
A força elástica é dada por:
A diferença vai ser dado pelo comprimento final da mola dado por menos o comprimento inicial, então:
Então para uma das molas temos:
Considerando as duas forças, temos:
Agora projetando essa força na direção teremos que multiplicar por e como ela aponta para o sentido negativo, a gente tem que:
Olhando a figura podemos expressar o cosseno da seguinte forma:
Então a gente encontra:
Passo 2
Agora vamos para o item .
Para encontrar a energia potencial vamos usar o fato de que:
Usando a expressão que encontramos para e usando o fato de que , assim:
Assim temos que:
Passo 3
Vamos para o item .
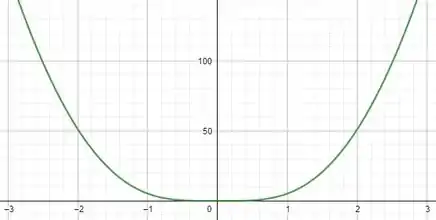
O gráfico de é mostrado abaixo.
Passo 4
Vamos para o item .
Vamos pegar a equação e fazer , assim:
Assim temos que:
Com isso podemos usar a conservação de energia, assim:
Usando a massa que o enunciado nos deu, temos:
Finalmente terminamos esse problema.
Resposta
Explicado acima.
Explicado acima.
